The Work Done by a Spring Force

To find an expression for the work done by the spring force as the block in Fig. 7-10a moves, let us make two simplifying assumptions about the spring. (1) It is massless; that is, its mass is negligible compared to the block's mass. (2) It is an ideal spring; that is, it obeys Hooke's law exactly. Let us also assume that the contact between the block and the floor is frictionless and that the block is particle-like.

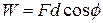We give the block a rightward jerk to get it moving, and then leave it alone. As the block moves rightward, the spring force does work on the block, decreasing the kinetic energy and slowing the block. However, we cannot find this work by using Eq. 7-7 ( ) because that equation assumes a constant force. The spring force is a variable force.

To find the work done by the spring, we use calculus. Let the block's initial position be 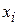and its later position 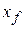. Then divide the distance between those two positions into many segments, each of tiny length 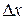. Label these segments, starting from 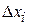as segments 1, 2, and so on. As the block moves through a segment, the spring force hardly varies because the segment is so short that hardly varies. Thus, we can approximate the force magnitude as being constant within the segment. Label these magnitudes as 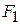in segment 1, 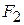in segment 2, and so on.

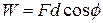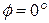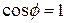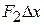With the force now constant in each segment, we can find the work done within each segment by using Eq. 7-7 ( ). Here , so . Then the work done is in segment 1, in segment 2, and so on. The net work 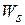done by the spring, from 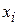- to 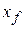, is the sum of all these works:

, (7-22)

where labels the segments. In the limit as 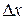goes to zero, Eq. 7-22 becomes

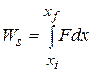(7-23)

Substituting for from Eq. 7-21, we find

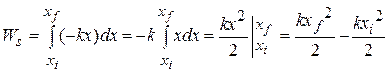
This work 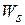done by the spring force can have a positive or negative value, depending on whether the net transfer of energy is to or from the block as the block moves from 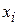to 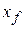,. Caution: The final position 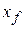appears in the second term on the right side of Eq. 7-25. Therefore, Eq. 7-25 tells us:

Work 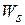is positive if the block ends up closer to the relaxed position ( 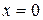) than it was initially. It is negative if the block ends up farther away from 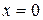. It is zero if the block ends up at the same distance from .

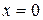If 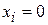and if we call the final position , then Eq. 7-25 becomes

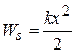(work by a spring force). (7-26)