The Concept of Forces
Everyone has a basic understanding of the concept of force from everyday experience. When you push your empty dinner plate away, you exert a force on it. Similarly, you exert a force on a ball when you throw or kick it. In these examples, the word force is associated with muscular activity and some change in the velocity of an object. Forces do not always cause motion, however. For example, as you sit reading this book, the force of gravity acts on your body and yet you remain stationary. As a second example, you can push (in other words, exert a force) on a large boulder and not be able to move it.
When a coiled spring is pulled, the spring stretches. When a stationary cart is pulled sufficiently hard that friction is overcome, the cart moves. When a football is kicked, as in it is both deformed and set in motion. These situations are all examples of a class of forces called contact forces. That is, they involve physical contact between two objects. Other examples of contact forces are the force exerted by gas molecules on the walls of a container and the force exerted by your feet on the floor.
Another class of forces, known as field forces, does not involve physical contact between two objects but instead act through empty space. Our present-day understanding of the physical world includes four distinct classes of forces. Two are familiar in everyday experience. The other two are concerned with interactions of fundamental particles. We cannot observe the latter with the unaided senses; studying them requires sophisticated and elaborate experiments.
Of the two familiar classes of force, gravitational interactionswere the first to be studied in detail. The weight of a body results from the earth's gravitational attraction acting on it. The sun's gravitational force on the earth is responsible for making the earth move in a nearly circular orbit instead of following a straight-line path as it would do if there were no force. Indeed, one of Newton's great achievements was to recognize that both the motions of the planets around the sun and the free fall of objects on earth are manifestations of gravitational forces.
The second familiar class of forces, electromagnetic interactions,includes electric and magnetic forces. When you run a comb through your hair, you can then use the comb to pick up bits of paper or fluff; this interaction is the result of electric charge on the comb. We encounter magnetic forces in interactions between magnets or between a magnet and a piece of iron. These may seem to fall in a different category, but detailed study shows that magnetic interactions are actually the result of electric charges in motion. An electromagnet causes magnetic interactions as a result of an electric current in a coil of wire.
These two familiar kinds of interactions differ enormously in their strength. For example, the electrical repulsion between two protons at a given distance apart is stronger than the gravitational attraction by a factor of the order of 1035. Thus gravitational forces play no significant role in determining the microscopic structure of atoms, molecules, and materials. But in bodies of astronomical size, protons and electrons are ordinarily present in nearly equal numbers; their charges are opposite and nearly cancel out. Gravitational interactions are the dominant influence in the motion of planets and also in the internal structure of stars.
The other two classes of interactions are less familiar. One, the strong interaction,is responsible for holding the nuclei of atoms together. Nuclei contain electrically neutral and positively charged particles. The charged particles repel each other; a nucleus could not be stable if it were not for the presence of an attractive force of a different kind that counteracts the repulsive electrical interactions. In this context the strong interaction is also called the nuclear force. It has shorter range than electrical interactions, but within its range it is much stronger.
Finally, there are the weak interactions;they play no direct role in the behavior of ordinary matter but are of vital importance in interactions among fundamental particles. The weak interaction is responsible for the emission of electrons (beta particles) from radioactive nuclei. In a beta-emitting nucleus a neutron is converted into a proton, an electron, and a third particle called a neutrino. The weak interaction is also responsible for the decay of many unstable particles produced in high-energy collisions of fundamental particles.
Since about 1970, attempts have been made to understand all four classes of interactions on the basis of a single unified theory called a grand unified theory. Such theories are still very speculative; as yet none has been completely successful.
Force
Force is a central concept in all of physics. Force is a measure of interaction/ /A force on a body resulting from direct contact with another body is called a contact force.For example, when wepush or pull on a body, we exert a force on it. A stretched spring exerts forces on the bodies attached to its ends; compressed air exerts a force on the wall of its container; and a locomotive exerts a force on the train it is pulling or pushing. Viewed on an atomic scale, contact forces result principally from the electrical attractions and repulsions of the electrons and nuclei in the atoms of the materials.
In contrast, gravitational forces, as well as electric and magnetic forces, can act through empty space; bodies do not have to be in contact for these forces to act.
Force is a vector quantity. This means that to describe a force, we need to describe the direction in which it acts as well as its magnitude, the quantity that describes "how much" or "how hard" the force pushes. We define units of force in terms of the units of mass, length, and time. The SI unit of force is the Newton, abbreviated N/
A familiar instrument for measuring forces is the spring balance. It consists of a coil spring, enclosed in a case for protection, with a pointer attached to one end. When forces are applied to the ends of the spring, it stretches; the amount of stretch depends on the force. We can calibrate such an instrument by using a number of identical bodies, each having a weight of exactly 1 N.

|
Suppose we slide a box along the floor by pulling it with a string or pushing it with a stick, as in Fig. 1. The interaction of the box with the
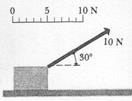 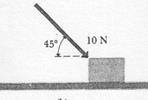
|
other bodies that push or pull it is described in terms of the forces they exert on the box. Thus our point of view is that the motion of the box is caused by the forces these bodies exert on it. The forces in the two cases can be represented as in Fig. 2. The labels indicate the magnitude and direction of the force; the length of the arrow, to some chosen scale, also shows the magnitude.
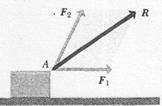
What happens when two forces, represented by the vectors 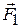 and
and 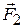 in Fig. 3, are applied simultaneously at the same point A of a body? Is it possible to produce the same effect on the body by applying a single force at A? If so, what should be its magnitude and direction?
in Fig. 3, are applied simultaneously at the same point A of a body? Is it possible to produce the same effect on the body by applying a single force at A? If so, what should be its magnitude and direction?
|
These questions can be answered only by experiment. Investigation shows that a single force equal to the vector sum 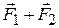 of the original forces produces the same effect as the two forces together. This single force is often called the resultantof the two forces. Hence the mathematical process of vector addition of two force vectors corresponds to the physical operation of finding the resultant of two forces, simultaneously applied at a given point. The same statement can be extended to combining any number of forces.
of the original forces produces the same effect as the two forces together. This single force is often called the resultantof the two forces. Hence the mathematical process of vector addition of two force vectors corresponds to the physical operation of finding the resultant of two forces, simultaneously applied at a given point. The same statement can be extended to combining any number of forces.
The fact that forces can be combined by vector addition is of the utmost importance. Furthermore, this fact also allows us to represent a force by means of components, as we have done with displacements/. In Fig. 4a, force  acts on a body at point 0. The components of
acts on a body at point 0. The components of  in the directions
in the directions 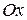 and
and 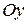 are
are 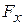 and
and 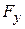 ; we find that simultaneous application of the forces
; we find that simultaneous application of the forces 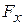 and
and 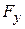 , as in Fig. 4b, is equivalent in all respects to the effect of the original force.
, as in Fig. 4b, is equivalent in all respects to the effect of the original force.
|
Any force can be replaced by its components, acing at the same point.
Forces can be represented by component:  ,
, 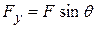 .
.
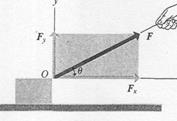
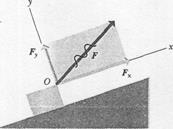
The axes we use to obtain components of a vector need not be vertical and horizontal. For example, Fig. 5 shows a block being pulled up an inclined plane by a force 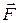 , represented by its components
, represented by its components 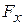 and
and 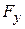 , parallel and perpendicular to the sloping surface of the plane.
, parallel and perpendicular to the sloping surface of the plane.
|
We will often need to find the vector sum of several forces acting on a body, which again may be called their resultant. The Greek letter 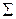 (sigma) is often used in a shorthand notation for this sum. If the forces are labeled
(sigma) is often used in a shorthand notation for this sum. If the forces are labeled  ,
,  ,
,  , and so on, and their resultant is
, and so on, and their resultant is 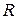 , then the operation
, then the operation
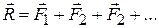 ,
,
is often abbreviated
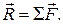
where 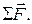 is read “the sum of the forces”. This means, of course, the vector sum. In terms of components, we may write
is read “the sum of the forces”. This means, of course, the vector sum. In terms of components, we may write
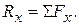 ,
, 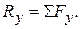
in which 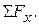 is read "the sum of the x-components of the forces."
is read "the sum of the x-components of the forces."
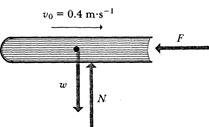
Example 4-3 A student shoves a lab notebook of mass 0.2 kg toward the right along a level lab bench. As the book leaves contact with the student's hand, it has an initial velocity of 0.4 m/s. As it slides, it slows down because of the horizontal friction force exerted on it by the bench top. It slides a distance of 1.0 m before coming to rest. What are the magnitude and direction of the friction force 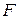 acting on it?
acting on it?
|
Solution. Suppose the book slides along the 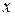 -axis in the +
-axis in the + 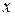 -direction, starting at the point
-direction, starting at the point 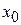 with the given initial velocity. A free-body diagram is shown in Fig. 4-11. We assume that the friction force is constant. The acceleration is then constant also. From the equations of motion with constant acceleration, we have
with the given initial velocity. A free-body diagram is shown in Fig. 4-11. We assume that the friction force is constant. The acceleration is then constant also. From the equations of motion with constant acceleration, we have
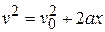 = (0.4 m/s)2 + (2a)(1.0 m);
= (0.4 m/s)2 + (2a)(1.0 m); 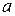 = -0.08 m/s2.
= -0.08 m/s2.
The negative sign means that the acceleration is toward the left (although the velocity is toward the right). The friction force on the book is
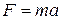 = (0.2 kg)(-0.08 m/s2) = -0.016 N,
= (0.2 kg)(-0.08 m/s2) = -0.016 N,
and is toward the left also. (A force of equal magnitude, but directed toward the right, is exerted on the table by the sliding book.)
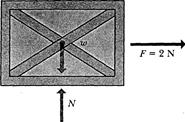
Example 4—4 A machine part having a mass of 5 kg slides along a rail aligned with the 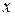 -axis. Its position is given as a function of time by
-axis. Its position is given as a function of time by
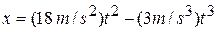 .
.
Find the force acting on the body, as a function of time. What is the force at time 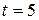 s? For what times is the force positive? Negative? Zero?
s? For what times is the force positive? Negative? Zero?
|
Solution. The free-body diagram is just like that of Example 4-2. We first find the acceleration a by taking the second derivative of 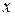 :
:
 .
.
Then, from Newton's second law,
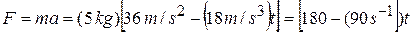 N.
N.
At time 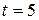 s, the force is
s, the force is 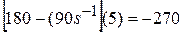 N. The force is zero when
N. The force is zero when 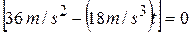 , that is, when
, that is, when 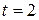 s. When
s. When  s,
s, 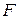 is positive,-and when
is positive,-and when 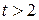 s,
s, 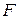 is negative.
is negative.
EXAMPLE 8—1 A particle of mass 2 kg moves along the 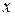 -axis with an initial velocity of 3 m/s. A force
-axis with an initial velocity of 3 m/s. A force 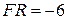 N (i.e., in the negative
N (i.e., in the negative 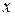 -direction) is applied for a period of 3 s. Find the final velocity.
-direction) is applied for a period of 3 s. Find the final velocity.
SolutionFrom Eq. (8-4),
(-6 N)(3 s) = (2 kg)  - (2 kg)(3 m/s),
- (2 kg)(3 m/s),
or
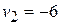 m/s.
m/s.
The particle's final velocity is in the negative 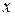 -direction.
-direction.
5-1 FORCESIN NATURE
Our present-day understanding of the physical world includes four distinct classes of forces. Two are familiar in everyday experience. The other two are concerned with interactions of fundamental particles. We cannot observe the latter with the unaided senses; studying them requires sophisticated and elaborate experiments.
Of the two familiar classes of force, gravitational interactionswere the first to be studied in detail. The weight of a body results from the earth's gravitational attraction acting on it. The sun's gravitational force on the earth is responsible for making the earth move in a nearly circular orbit instead of following a straight-line path as it would do if there were no force. Indeed, one of Newton's great achievements was to recognize that both the motions of the planets around the sun and the free fall of objects on earth are manifestations of gravitational forces.
The second familiar class of forces, electromagnetic interactions, includes electric and magnetic forces. When you run a comb through your hair, you can then use the comb to pick up bits of paper or fluff; this interaction is the result of electric charge on the comb. We encounter magnetic forces in interactions between magnets or between a magnet and a piece of iron. These may seem to fall in a different category, but detailed study shows that magnetic interactions are actually the result of electric charges in motion. An electromagnet causes magnetic interactions as a result of an electric current in a coil of wire. We will study electric and magnetic interactions in detail in the second half of this book.
These two familiar kinds of interactions differ enormously in their strength. For example, the electrical repulsion between two protons at a given distance apart is stronger than the gravitational attraction by a factor of the order of 1035. Thus gravitational forces play no significant role in determining the microscopic structure of atoms, molecules, and materials. But in bodies of /astronomical size, protons and electrons are ordinarily present in nearly equal numbers; their charges are opposite and nearly cancel out. Gravitational interactions are the dominant influence in the motion of planets and also in the /internal structure of stars.
The other two classes of interactions are less familiar. One, the strong interaction, is responsible for holding the nuclei of atoms together. Nuclei contain electrically neutral and positively charged particles. The charged particles repel each other; a nucleus could not be stable if it were not for the presence of an attractive force of a different kind that counteracts the repulsive electrical interactions. In this context the strong interaction is also called the nuclear force. It has shorter range than electrical interactions, but within its range it is much stronger.
Finally, there are the weak interactions; they play no direct role in the behavior of ordinary matter but are of vital importance in interactions among fundamental particles. The weak interaction is responsible for the emission of electrons (beta particles) from radioactive nuclei. In a beta-emitting nucleus a neutron is converted into a proton, an electron, and a third particle called a neutrino. The weak interaction is also responsible for the decay of many unstable particles produced-in high-energy collisions of fundamental particles. Since about 1970, attempts have been made to understand all four classes of interactions on the basis of a single unified theory called grand unified theory. Such theories are still very speculative, as yet none has been completely successful. In 1983, however, evidence was found that supports a unified theory of the electromagnetic and weak interactions. The entire area is a very active field of present-day theoretical and experimental research.
Дата добавления: 2015-06-17; просмотров: 1074;
