Relative Motion in One Dimension

Suppose you see a duck flying north at, say, 30 km/h. To another duck flying alongside, the first duck seems to be stationary. In other words, the velocity of a particle depends on the reference frameof whoever is observing or measuring the velocity. For our purposes, a reference frame is the physical object to which we attach our coordinate system. In everyday life, that object is the ground. For example, the speed listed on a speeding ticket is always measured relative to the ground. The speed relative to the police officer would be different if the officer were moving while making the speed measurement.

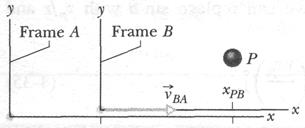
Fig. 4-20Alex (frame A) and Barbara (frame B) watch car P, as both В and P move at different velocities along the common 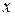axes of the two frames. At the instant shown, 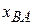is the coordinate of В in the A frame. Also, P is at coordinate 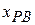in the В frame and coordi­nate in the A frame.

Suppose that Alex (at the origin of frame A) is parked by the side of a highway, watching car P (the "particle") speed past. Barbara (at the origin of frame B) is driving along the highway at constant speed and is also watching car P. Suppose that, as in Fig. 4-20, they both measure the position of the car at a given moment. From the figure we see that

(4-38)

The equation is read: "The coordinate 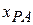of P as measured by A is equal to the coordinate 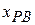of P as measured by В plus the coordinate 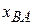of В as measured by A." Note how this reading is supported by the sequence of the subscripts. Taking the time derivative of Eq. 4-38, we obtain

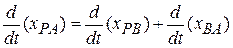
Or (because )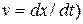

(4-39)

This equation is read: "The velocity 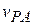of P as measured by A is equal to the velocity 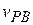of P as measured by В plus the velocity of В as measured by A." The term is the velocity of frame В relative to frame A. (Because the motions are along a single axis, we can use components along that axis in Eq. 4-39 and omit overhead vector arrows.)

Here we consider only frames that move at constant velocity relative to each other. In our example, this means that Barbara (frame B) will drive always at constant velocity relative to Alex (frame A). Car P (the moving particle), however, may speed up, slow down, come to rest, or reverse direction (that is, it can accelerate).

To relate an acceleration of P as measured by Barbara and by Alex, we take the time derivative of Eq. 4-39:

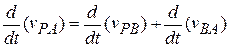(4-40)

Because is constant, the last term is zero and we have

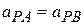. In other words.

► Observers on different frames of reference (that move at constant velocity relative to each other) will measure the same acceleration for a moving particle.