Relative Motion in Two Dimensions
Now we turn from relative motion in one dimension to relative motion in two (and, by extension, in three) dimensions. In Fig. 4-21, our two observers are again watching a moving particle P from the origins of reference frames A and B, while В moves at a constant velocity  relative to A. (The corresponding axes of these two frames remain parallel.)
relative to A. (The corresponding axes of these two frames remain parallel.)
Figure 4-21 shows a certain instant during the motion. At that instant, the position vector of В relative to A is 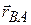 . Also, the position vectors of particle P are
. Also, the position vectors of particle P are  relative to A and
relative to A and  relative to B. From the arrangement of heads and tails of those three position vectors, we can relate the vectors with
relative to B. From the arrangement of heads and tails of those three position vectors, we can relate the vectors with
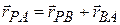 (4-41)
(4-41)
|
The plane has velocity 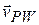 relative to the wind, with an airspeed (speed relative to the wind) of 215 km/h, directed at angle
relative to the wind, with an airspeed (speed relative to the wind) of 215 km/h, directed at angle 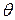 south of east. The wind has velocity
south of east. The wind has velocity  relative to the ground, with a speed of 65.0 km/h, directed 20.0° east of north. What is the magnitude of the velocity
relative to the ground, with a speed of 65.0 km/h, directed 20.0° east of north. What is the magnitude of the velocity  of the plane relative to the ground, and what is 0?
of the plane relative to the ground, and what is 0?
|
Fig. 4-21 Frame В has the constant two-dimensional velocity 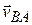 relative to frame A. The position vector of В relative to A is
relative to frame A. The position vector of В relative to A is 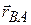 . The position vectors of particle P are
. The position vectors of particle P are  relative to A and
relative to A and  relative to B.
relative to B.
By taking the time derivative of this equation, of particle P we can relate the velocities 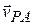 and
and 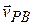
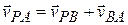
By taking the time derivative of this relation, we can relate the accelerations 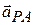 and
and 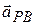 of the particle P relative to our observers. However, note that because
of the particle P relative to our observers. However, note that because 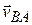 is constant, its time derivative is zero. Thus, we get
is constant, its time derivative is zero. Thus, we get

As for one-dimensional motion, we have the following rule: Observers on different frames of reference that move at constant velocity relative to each other will measure the same acceleration for a moving particle.
 Sample Problem 4-11
Sample Problem 4-11
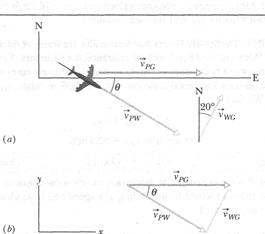
In Fig. 4-22a, a plane moves due east (directly toward the east) while the pilot points the plane somewhat south of east, toward a steady wind that blows to the northeast. SOLUTION: The Key Idea is that the situation is like the one in Fig. 4-21. Here the moving particle P is the plane, frame A is attached to the ground (call it 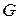 ), and frame В is "attached" to the wind (call it
), and frame В is "attached" to the wind (call it 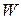 ). We need to construct a vector diagram like that in Fig. 4-21 but this time using the three velocity vectors.
). We need to construct a vector diagram like that in Fig. 4-21 but this time using the three velocity vectors.
First construct a sentence that relates the three vectors:

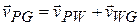
We want the magnitude of the first vector and the direction of the second vector. With unknowns in two vectors, we cannot solve Eq. 4-44 directly on a vector-capable calculator. Instead, we need to resolve the vectors into components on the coordinate system of Fig. 4-226, and then solve Eq. 4-44 axis by axis (see Section 3-5). For the у components, we find
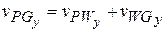
or 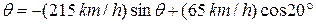

Solving for 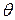 gives us
gives us
 (Answer)
(Answer)
Similarly, for the 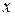 components we find
components we find
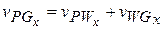
Here, because  is parallel to the
is parallel to the 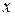 axis, the component
axis, the component 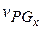 is equal to the magnitude
is equal to the magnitude 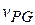 . Substituting this and
. Substituting this and 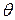 =16.5°, we find
=16.5°, we find
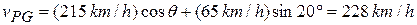 (Answer)
(Answer)
A body moves in a straight line along 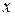 -axis. Its distances
-axis. Its distances 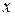 (in meter) from the origin is given by
(in meter) from the origin is given by 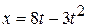 . The average speed in the interval
. The average speed in the interval 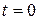 to
to 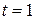 second is
second is
(A) 5 m/s (B) -4 m/s
(C) 6 m/s (D) zero
A particle moves along 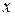 -axis in such a way that its coordinate
-axis in such a way that its coordinate 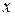 vanes with time t according to the expression
vanes with time t according to the expression 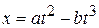 . The acceleration of the particle will be zero at time
. The acceleration of the particle will be zero at time
(A) 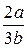 (B)
(B) 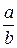 (C)
(C)  (D) zero
(D) zero
A particle moves along a straight line, such that its displacement 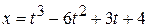 (in metres). The velocity, when the acceleration is zero, is
(in metres). The velocity, when the acceleration is zero, is
(A) -12 m/s (B) -9 m/s (C) 3 m/s (D) 42 m/s
The equation 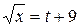 gives the variation of displacement with time. Which of the following is correct?
gives the variation of displacement with time. Which of the following is correct?
(A) Velocity is proportional to time.
(B) Velocity is inversely proportional to time.
(C) Acceleration depends upon time.
(D) Acceleration is constant.
A particle moving along a straight line has a velocity  m/s, when it cleared a distance of x meters. These two are connected by the relation
m/s, when it cleared a distance of x meters. These two are connected by the relation  . When its velocity is l m/s, its acceleration (in m s-2) is :
. When its velocity is l m/s, its acceleration (in m s-2) is :
(A) 2 (B) 7 (C) 1 (D) 0.5
If 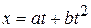 , where x is the distance traveled by the body kilometers, while t is time in seconds, then units of b
, where x is the distance traveled by the body kilometers, while t is time in seconds, then units of b
(A) km/s (B) km·s (C) km/s2 (D) km·s2
An acceleration of a particle is increasing linearly with time  as
as 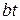 The particle starts from the origin with an initial velocity
The particle starts from the origin with an initial velocity 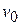 . The distance traveled by the particle in time
. The distance traveled by the particle in time  will be
will be
(A)  (B)
(B) 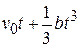 (C)
(C) 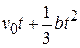 (D)
(D) 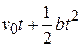
Дата добавления: 2015-06-17; просмотров: 1004;
