GRAVITATIONAL FIELD

Newton's law of gravitation can be restated in a useful way with the concept of gravitational field.Instead of calculating the interaction forces between two masses by using Eq. (6—11) directly, we consider a two-stage process. First, we think of one mass as creating a change at each point in the space surrounding it. This change is called a gravitational field. To describe it, we associate a vector quantity 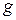with each point in space. The significance of 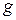is that a particle of mass m at a point where the gravitational field is 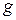experiences a gravitational force given by 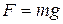. To measure a gravitational field we may place a small mass, called a test mass, at the point. If the mass experiences a gravitational force, then there is a gravitational field at that point.

In Example 6-8, instead of calculating directly the forces on the 0.001-kg body by the large bodies, we may take the point of view that the large bodies create a gravitational field at the location of the small body, and that the field exerts a force on any mass located at the point.

Because force is a vector quantity, gravitational field is also a vector quantity. We define the gravitational field 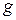at a point as the quotient of the force 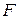experienced by a test mass 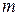and the mass. Thus

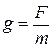(6-17)

To say it another way: At a point where the gravitational field is 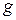, the force 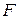on a mass 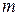is given by

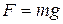(6-18)

The gravitational field due to a point mass 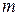, at a distance 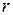away from it, has magnitude

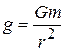(6-19)

and is directed toward the point mass. Gravitational fields also obey the principle of superposition: The total gravitational field at a point, due to several point masses, is the vector sum of the gravitational fields of the separate masses. Gravitational field is a very useful concept; when we know the field, we can calculate quickly the gravitational force on any body.

The gravitational field in the vicinity of any collection of masses varies from one point to another in the region. Thus it is not a single vector quantity but rather a whole collection of vector quantities, one vector associated with each point in space. Indeed, this is what is meant by the general term vector field. Another familiar example of a vector field is the velocity in a flowing fluid: different parts of the fluid have different velocities, and so we speak of the velocity field in the fluid. During our study of electricity and magnetism, we will discuss in detail the properties of the electric and magnetic fields; both of these are vector fields.