The Linear Momentum of a System of Particles

Now consider a system of 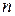particles, each with its own mass, velocity, and linear momentum. The particles may interact with each other, and external forces may act on them as well. The system as a whole has a total linear momentum , which is defined to be the vector sum of the individual particles' linear momenta. Thus,

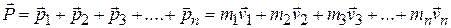(9-24)

If we compare this equation with Eq. 9-17, we see that

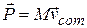(linear momentum, system of particles), (9-25)

which gives us another way to define the linear momentum of a system of particles:

The linear momentum of a system of particles is equal to the product of the total mass 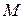of the system and the velocity of the center of mass.

If we take the time derivative of Eq. 9-25, we find

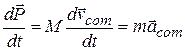(9-26)

Comparing Eqs. 9-14 and 9-26 allows us to write Newton's second law for a system of particles in the equivalent form

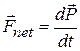(9-27)

where 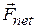is the net external force acting on the system. This equation is the gen­eralization of the single-particle equation 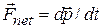to a system of many particles.

9-6 Conservation of Linear Momentum

Suppose that the net external force acting on a system of particles is zero (the system is isolated) and that no particles leave or enter the system (the system is closed). Putting 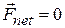in Eq. 9-27 then yields 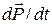, or

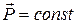(closed, isolated system). (9-29)

In words,

If no net external force act on a system of particles, the total linear momentum 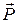of the system cannot change.

This result is called the law of conservation of linear momentum.It can also be written as

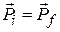(closed, isolated system). (9-30)

In words, this equation says that, for a closed, isolated system,

(total linear momentum at some initial time 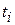) = (total linear momentum\ at some later time )

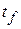Equations 9-29 and 9-30 are vector equations and, as such, each is equivalent to three equations corresponding to the conservation of linear momentum in three mutually perpendicular directions as in, say, the xyz coordinate system. Depending on the forces acting on a system, linear momentum might be conserved in one or two directions but not in all directions. However,

It the component of the net external force on a closed system is zero along an axis, then the component of the linear momentum of the system along that axis cannot change.

As an example, suppose that you toss a grapefruit across a room. During its flight, the only external force acting on the grapefruit (which we take as the system) is the gravitational force 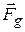, which is directed vertically downward. Thus, the vertical component of the linear momentum of the grapefruit changes, but since no horizontal external force acts on the grapefruit, the horizontal component of the linear momentum cannot change.

Note that we focus on the external forces acting on a closed system. Although internal forces can change the linear momentum of portions of the system, they cannot change the total linear momentum of the entire system.

•CHECKPOINT 4: An initially stationary device lying on a frictionless floor explodes into two pieces, which then slide across the floor. One piece slides in the positive direction of an x axis, (a) What is the sum of the momenta of the two pieces after the explosion? (b) Can the second piece move at an angle to the x axis? (c) What is the direction of the momentum of the second piece?

Sample Problem 9-5

A ballot box with mass 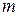= 6.0 kg slides with speed 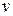= 4.0 m/s across a frictionless floor in the positive direction of an x axis. It suddenly explodes into two pieces. One piece, with mass 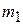= 2.0 kg, moves in the positive direction of the x axis with speed 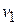= 8.0 m/s. What is the velocity of the second piece, with mass ?

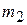SOLUTION: There are two Key Ideas here. First, we could get the velocity of the second piece if we knew its momentum, because we already know its mass is 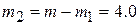kg. Second, we can relate the momenta of the two pieces to the original momentum of the box if momentum is conserved. Let's check.

Our reference frame will be that of the floor. Our system, which consists initially of the box and then of the two pieces, is closed but is not isolated, because the box and pieces each expellee a normal force from the floor and a gravitational force. However, those forces are both vertical and thus cannot change the horizontal component of the momentum of the system. Neither can the forces produced by the explosion, because those forces are internal to the system. Thus, the horizontal component of the momentum of the system is conserved, and we can apply Eq. 9-30 along the x axis.

The initial momentum of the system is that of the box:

.

Similarly, we can write the final momenta of the two pieces as

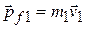and .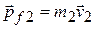

The final total momentum 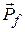of the system is the vector sum of the momenta of the two pieces:

.

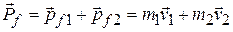Since all the velocities and momenta in this problem are vectors along the x axis, we can write them in terms of their x components. Doing so while applying Eq. 9-30, we now obtain

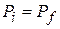
Or .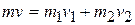

Inserting known data, we find

(6.0 kg)(4.0 m/s) = (2.0 kg)(8.0 m/s) + (4.0 kg)v₂

and thus v₂ = 2.0 m/s. (Answer)

Since the result is positive, the second piece moves in the positive direction of the x axis.