ADVANCED LINEAR/NONLINEAR MODELS
Якщо за результатами аналізу дослідні дані не відповідають закону нормального розподілення (див. скористатись нелінійними методами, або провести відповідне перетворення даних.
Розглянемо порядок знаходження коефіцієнтів рівняння регресії нелінійного виду, які через перетворення змінних можуть бути наведені до лінійної моделі. Знайдемо параметри регресійного рівняння, що дозволяє розрахувати кількість вузлів на рослині (змінна SN) залежно від відносної вологості повітря (NB). Рівняння має вид: SN = a1 + a2 NB + a3 NB 2.
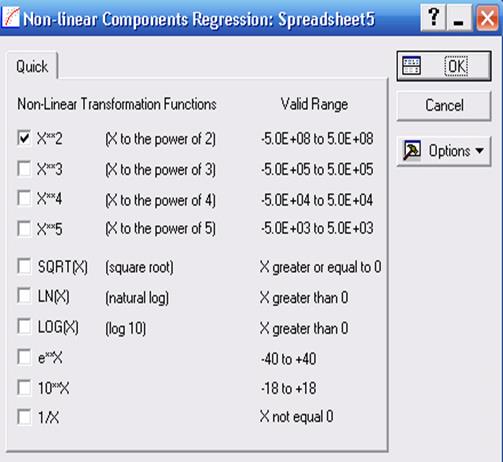
Для цього відкриємо функцію Fixed Nonlinear Regression вкладки Advanced Linear/Nonlinear models. Після вибору змінних і натискання на кнопку ОК, у діалоговому вікні Multiple Regressions з'являється вікно Non-linear Components Regression (рис. 15.1), у якому можна вибрати відповідний тип перетворення змінних.
|
| Рис. 15.1. Вікно вибору типів перетворення змінних |
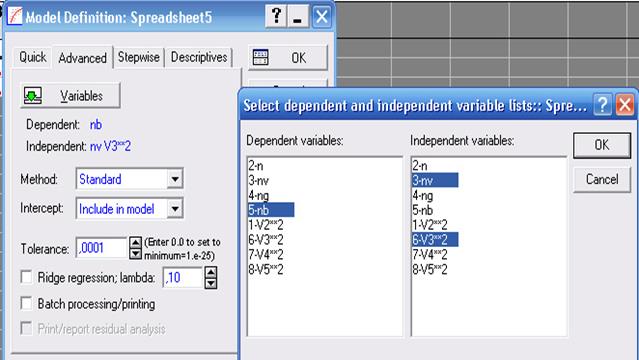
Після того, як тип перетворення змінних визначений (у нашому прикладі це зведення у квадрат), необхідно уточнити залежну й незалежні змінні фіксованої нелінійної регресійної моделі. Вони вибираються на наступному кроці за допомогою кнопки Variables діалогового вікна Model Definition (Уточнення моделі) (рис. 15.2).
|
| Рис.15.2. Діалогове вікно Model Definition (Уточнення моделі) |
Залежною (dependent) змінною в нашому випадку буде - SN; незалежними (independent) - NB і NB 2 (рис. 14.2). Змінна NB 2 значиться в списку змінних як V3**2, тому що змінна NB є другою в списку змінних.
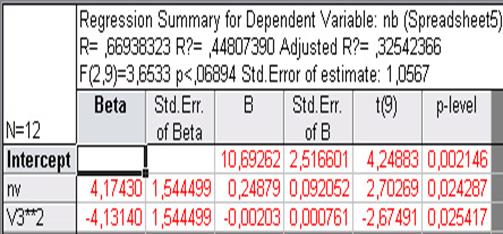
Рівняння регресії про кількість вузлів на рослині гороху (SN) залежно від відносної вологості повітря (NB) виявилося наступним: SN = 10,692 + 0,248 NB - 0,002 NB 2. Всі коефіцієнти рівняння значимі на 5% рівні значущості (p-level < 0,05). Це рівняння пояснює майже 44,8% (R2 = 0,448) варіації залежної змінної (рис. 15.3).
|
| Рис. 15.3. Результати регресійного аналізу моделі SN = a1 + a2 NB + a3 NB 2 |
Як видно з розрахунків, отримана модель, не зважаючи на те, що вона достовірна не повністю, пояснює взаємозв’язок між кількістю вузлів на рослині гороху від вологості повітря. Про що свідчить також аналіз залишків (рис 15.4).
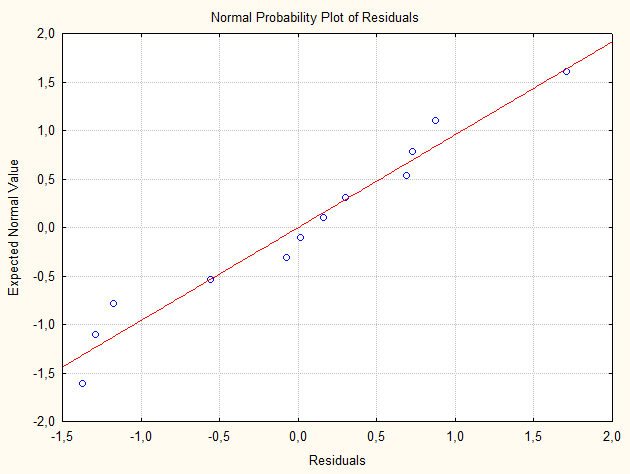 Рис. 15.4. Графік залишків на нормальному імовірнісному папері Рис. 15.4. Графік залишків на нормальному імовірнісному папері
|
Нелінійний тренд в регресійних залишках свідчить про необхідність перегляду моделі, тобто вибору іншого методу перетворення або уведення інших змінних.
Пошук найкращої регресійної моделі є досить громіздким процесом. Щоб його подолати, треба керуватися наступними вимогами (Дрейпер, Сміт, 1981):
1. Регресійна модель повинна пояснювати не менш 80% варіації залежної змінної, тобто R2³0,8.
2. Стандартна помилка оцінки залежної змінної рівняння повинна становити не більше 5% середнього значення залежної змінної;
3. Коефіцієнти рівняння регресії і його вільний член повинні бути
істотними на 5%-му рівні значущості.
4. Залишки від регресії повинні бути без помітної автокореляції (r<0,30), нормально розподілені й без систематичної складової.
Чим менше сума квадратів залишків, чим менше стандартна помилка оцінки й чим більше R2 , тим більш точним є рівняння регресії.
16. КЛАСТЕРНИЙ АНАЛІЗ (CLUSTER ANALYSIS)
На сьогоднішній день у сільськогосподарських науках багатомірним аналізам приділяється недостатньо уваги, тому у цьому розділі зупинимося на загальних аспектах, які допоможуть досліднику застосувати ці методи в своїх дослідженнях.
Найбільш часто у агрономічних дослідженнях застосовується кластерний аналіз. Термін кластерний аналіз уперше запровадив Tryon (1939). Він містить набір різних алгоритмів. Основне питання, що турбує дослідників при аналізі багатовимірних ознак, полягає в надані дослідним даним добру наочну структуру.
На відміну від багатьох інших статистичних процедур, кластерний аналіз використовують тоді, коли дослідник не має яких-небудь апріорних гіпотез щодо загальної оцінки варіантів досліджень. Концепція кластерного аналізу полягає у визначенні серед вихідної множини оптимального значення цільової функції. Більшість алгоритмів кластеризації побудовано на використанні евристичних методів, тому вибір їх зводиться до отримання найбільш корисного результату.
Найбільш часто використовується алгоритм деревоподібної кластерізації. Призначення цього алгоритму складається в певному об'єднанні об'єктів. Типовим результатом такої кластеризації є ієрархічне дерево.
Метод деревоподібної графіки використовується при формуванні кластерів відмінності або відстані між об'єктами. Ці відстані можуть визначатися в одномірному або багатомірному просторі. Найбільш просто відстані між об'єктами в одномірному або багатомірному просторах можна обчислити через евклідові відстані. У просторовому вимірі, що має вигляд двох або трьох осей, реальною геометричною віддаллю між об'єктами є ті, що можна визначити, скажімо, рулеткою.
У сільськогосподарських дослідженнях кластерний аналіз найбільш часто застосовується у селекції, рослинництві та інших науках. Наш приклад буде побудований на комплексній оцінці дії декількох систем удобрення озимої пшениці.
Схема досліду:
| 1- Контроль - без добрив |
| 2 - N120Р100К140 |
| 3 - N120Р100К140 + побічна продукція |
| 4 - N120Р100К140 + гній 40т/га |
| 5 - N60Р50К70 + гній 40т/га |
Для оцінки наведених систем удобрення були враховані наступні ознаки:
| Густота рослин, шт./м2. |
| Кількість продуктивних стебел, шт./м2. |
| Кількість зерен в колосі, шт. |
| Висота рослин, см. |
| Маса 1000 зерен, г. |
| Натура зерен, г/л. |
| Вміст білка, %. |
| Урожайність, т/га. |
У сформованому файлі “Кластерний аналіз” наведені ознаки розміщені стрічками (Case), а варіанти (Var) – колонками (рис.16.1).
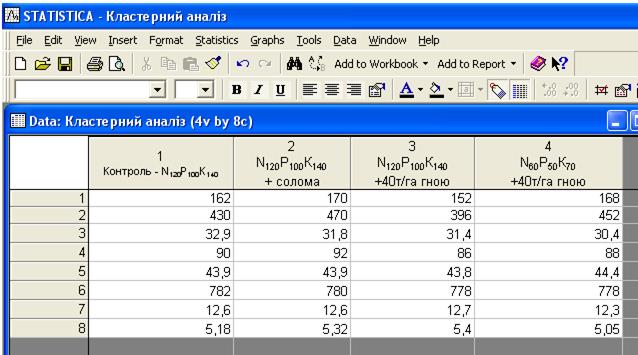
Рис 16.1. Формування файлу для кластерного аналізу
У верхньому меню обираємо пункт Statistics далі Multivariate Exploratory Techniques --> Cluster Analysis (рис. 16.2).

| Рис 16.2. Вибір опцій для кластерного аналізу |
З’являється вікно вибору методу кластерного аналізу (рис. 16.3), в якому обираємо опцію Joining (tree clustering). В цьому вікні є методиК-середніх (K-means clustering) та двовхідне об’єднання (Two way joining).
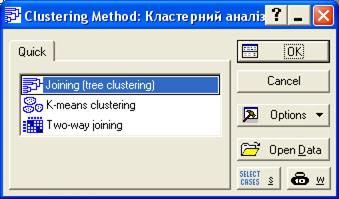
|
| Рис 16.3. Вікно вибору методу кластерного аналізу |
 Далі з’являється вікно вибору параметрів деревоподібної кластеризації. Переходимо на вкладку (Розширені параметри), де обираємо (рис.16.4):
Далі з’являється вікно вибору параметрів деревоподібної кластеризації. Переходимо на вкладку (Розширені параметри), де обираємо (рис.16.4):


Рис. 16.4. Вибір змінних для аналізу
- Input file – тип вхідного файлу – Raw data Дані у рядках (файл даних може бути представлений і як матриця кореляцій)
- Cluster – що об’єднувати у кластер – Cases (raws) – Рядки (якби у нас був інший файл даних, можливо було б об’єднувати у кластери стовпчики)
- Amalgamation (linkage) rule – правила об’єднання – Single linkage (Просте об’єднання)
- Distance measure – міра відстаней – Euclidean distances Евклідові відстані
Після вибору параметрів натискаємо кнопку ОК, з’являється вікно Select variables for the analysis Вибір змінних для аналізу (див. рис. з аналогічною назвою), де обираємо показники для аналізу. Натискаємо ОК, і отримуємо вікно з відображеними параметрами можливих результатів кластерного аналізу та кнопками, для визначення типу інтерпретації результатів (див. рис. 15.4, нижня таблиця).
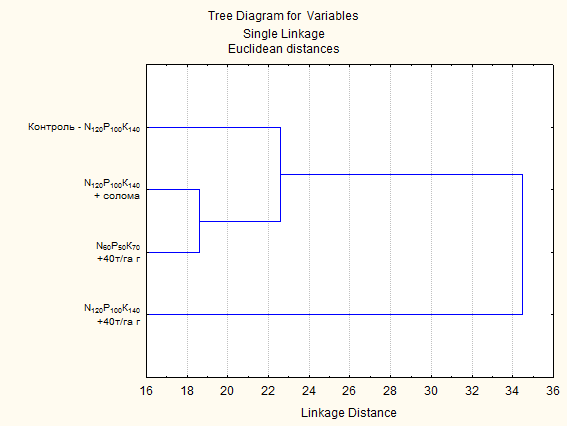
У абсолютній більшості випадків будують дерево кластеризації – це найбільш наглядний спосіб представлення результатів кластерного аналізу. Його можна побудувати у вигляді горизонтального (Horizontal hierarchical tree plot) або вертикального (Vertical icicle plot) дерева кластеризації. Горизонтальне дерево зазвичай будують при великій кількості варіантів (для селекції – вихідних форм, сортів, ліній). Для прикладу побудуємо горизонтальне ієрархічне дерево (рис. 16.5).
|
| Рис. 16.5. Графічне представлення результатів кластерного аналізу |
Кластери (групи) за віддалями визначені за методом “найближчого сусіда ”: чим нижче горизонтальна лінія відносно осі Х, тим найменші віддалі між цими варіантами
Висновок. За комплексною оцінкою систем удобрення на урожайність озимої пшениці найбільш близькими за структурою були варіанти сумісного внесення 40 т/га гною + N60P50K70 і N120P100K140 + солома. Варіант внесення 40 т/га гною + N120P100K140 за комплексом ознак найбільш різниться серед досліджуваних варіантів.
Наведений висновок буде аналогічним, якщо подати ці ж дані у вигляді Graf of amalgamation schedule - покрокове розміщення або Distance matrix - дистанційна матриця.
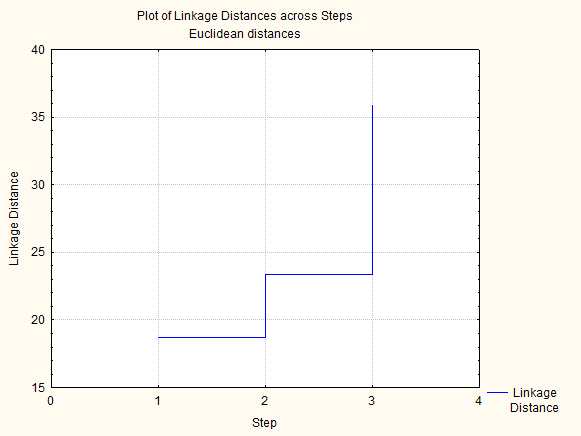
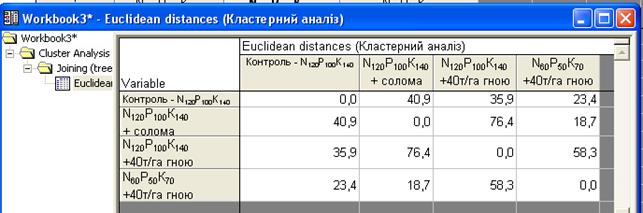
|
Рис. 16.6. Інші форми представлення результатів кластерного аналізу
Отже, проведення статистичних аналізів за допомогою пакету Statistica 6.0 дозволяє зосередити увагу не на рутинних обчисленнях за складними формулами, а на безпосередньому аналізі результатів досліджень розуміння впливу факторів досліду на кінцеву ознаку, взаємодії факторів, та виділенні найбільш сприятливих варіантів, їх теоретичному обґрунтуванні на основі біологічних знань.
Дата добавления: 2015-04-25; просмотров: 1416;
