MULTIPLE LINEAR REGRESSIONS
Кількісна залежність між факторами визначається за рівнянням регресії.
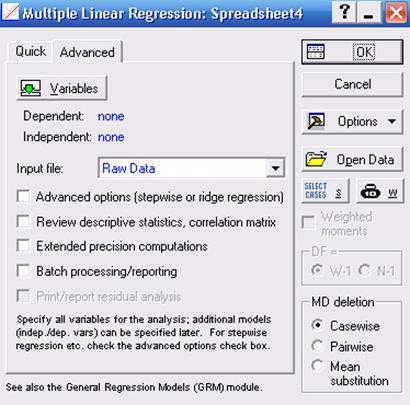
У стартовому діалоговому вікні цього модуля (рис. 14.1) за допомогою кнопки Variables вказуються залежна (dependent) і незалежні (незалежна) (independent) змінні. У полі Input file вказується тип файлу з даними:
Raw Date - дані у вигляді рядкової таблиці;
Correlation Matrix - дані у вигляді кореляційної матриці.
|
| Рис.14.1. Стартове діалогове вікно модуля Multiple Linear Regressions |
У поле MD deletion вказується спосіб виключення з обробки відсутніх даних:
casewise - ігнорується весь рядок, у якому є хоча б одне пропущене значення;
mean substitution - замість пропущених даних підставляються середні значення змінних;
pairwise - попарне виключення даних із пропусками тих змінних, кореляція яких обчислюється.
Використання цього типу аналізу передбачає створення стандартної лінійної моделі виду:
Y = a1 + a2X1 + a3X2 + a3X3 + ……+ anXn
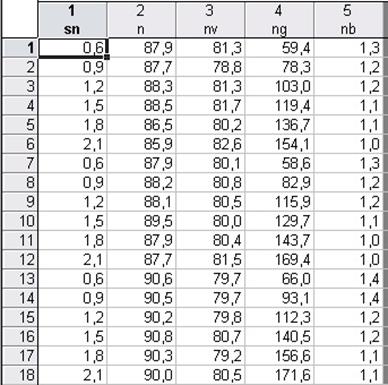
Розглянемо проведення регресійного аналізу на прикладі. Є дані структурних показників посівів гороху . У файлі даних (рис. 14.2) 5 змінних:
| sn | Густота рослин, млн. шт./га | |
| n | Польова схожість насіння, % | |
| nv | Виживання за вегетаційний період, % | |
| ng | Кількість пагонів, шт. /м | |
| nb | Гілкування |
|
| Рис.14.2. Вид вікна з файлом даних |
Знайдемо параметри регресійного рівняння лінійного зв'язку густоти рослин від польової схожості і кількості пагонів. Вид рівняння: SN = a1 + a2N + a3NG.
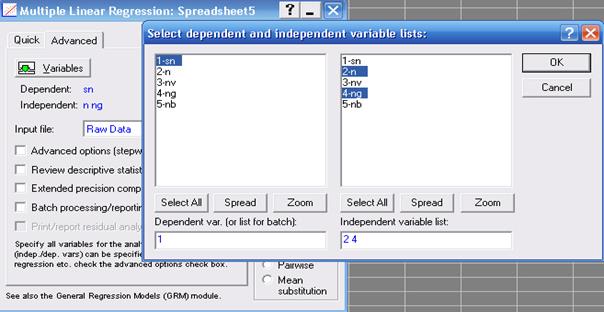
Виставимо опції стартового вікна регресійного аналізу (рис.45):
Variables: залежна (dependent) змінна - SN; незалежні (independent) – N, NG;
Input file - Raw Date (дані файлу у вигляді рядкової таблиці); MD deletion - pairwise.
|
| Рис. 14.3. Вибір залежної й незалежних змінних |
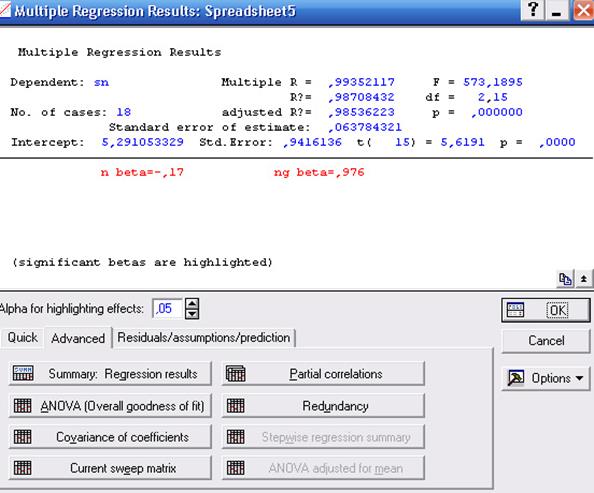
Після того, як всі опції стартового діалогового вікна регресійного аналізу виставлені, натискання на кнопку ОК призводить до появи вікна Multiple Regressions Results (результати регресійного аналізу, рис. 14.4), за допомогою якого можна переглянути результати аналізу в деталях.
|
| Рис. 14.4. Вікно результатів регресійного аналізу |
У верхній частині вікна приводяться найбільш важливі параметри отриманої регресійної моделі:
Multiple R - коефіцієнт множинної кореляції, що характеризує тісноту лінійного зв'язку між залежною й всіма незалежними змінними. Може приймати значення від 0 до 1.
R2 або RI - коефіцієнт детермінації - виражає частку варіації залежної змінної, визначену регресійним рівнянням. Чим більше R2, тим більшу частку варіації пояснюють змінні, включені в модель.
Аdjusted R - скоректований коефіцієнт множинної кореляції, він позбавлений недоліків коефіцієнту множинної кореляції. Включення нової змінної в регресійне рівняння не завжди збільшує RI, а тільки в тому випадку, коли F-критерій при перевірці гіпотези про значимість включеної змінної більше або дорівнює 1, інакше включення нової змінної зменшує значення RI і adjusted R2 .
Аdjusted R2 або adjusted RI - скоректований коефіцієнт детермінації, можна з більшим успіхом (у порівнянні з R2) застосовувати для вибору найкращої підмножини незалежних змінних у регресійному рівнянні
F - F-критерій.
df - число ступенів волі для F-критерію.
p - імовірність нульової гіпотези для F-критерію.
Standard error of estimate - стандартна помилка оцінки (рівняння).
Intercept - вільний член рівняння.
Std.Error - стандартна помилка вільного члена рівняння.
t - t-критерій для вільного члена рівняння.
p - імовірність нульової гіпотези для вільного члена рівняння.
Beta - стандартизовані регресійні коефіцієнти рівняння, розраховані за стандартизованим значенням змінних. За їхньою величиною можна зрівняти й оцінити значимість залежних змінних. Β - коефіцієнт показує на скільки одиниць стандартного відхилення зміниться залежна змінна при зміні на одне стандартне відхилення незалежної змінної за умови сталості інших незалежних змінних. Вільний член у такому рівнянні дорівнює 0.
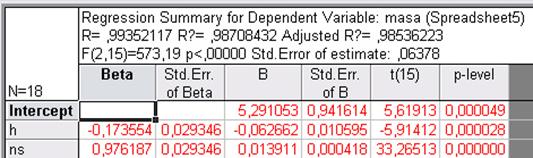
Кнопка Summary regression results - дозволяє отримати основні результати регресійного аналізу (рис. 13.5): BETA - коефіцієнти рівняння; St. Err. of BETA - стандартні помилки β- коефіцієнтів; В - коефіцієнти рівняння регресії; St. Err. of B - стандартні помилки коефіцієнтів рівняння регресії; t (95) - t-критерії для коефіцієнтів рівняння регресії; р-level - імовірність нульової гіпотези для коефіцієнтів рівняння регресії.
|
| Рис. 14.5. Основні результати регресійного аналізу |
У такий спосіб отримане наступне рівняння регресії, яке визначає залежність густоти рослин (SN) від польової схожості (N) і кількості пагонів (NG):
N = 5,29 - 0,062N + 0,013NS.
Усі коефіцієнти рівняння є істотними на 5% рівні (p-level < 0,05). Це рівняння діє у 98,7% випадків вибірки (R2 = 0,987).
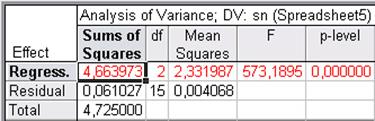
Це можна перевірити на підставі дисперсійного аналізу. Кнопка ANOVA (дисперсійний аналіз) - дозволяє проаналізувати рівняння регресії (рис. 13.6). У рядках таблиці дисперсійного аналізу рівняння регресії - джерела варіації: Regress. - обумовлена регресією, Residual- залишкова, Total - загальна. У стовпцях таблиці: Sums of Squares - сума квадратів, df - число ступенів волі, Mean Squares - середній квадрат, F - значення F - критерію, p-level - імовірність нульової гіпотези для F - критерію.
|
| Рис.14.6. Результати дисперсійного аналізу рівняння регресії |
Отже, F - критерій рівняння регресії істотний на 5% рівні значущості. Імовірність нульової гіпотези (p-level) значно менше 0,05, що говорить про загальну значимість рівняння регресії.
Кнопка Partial correlations - дозволяє переглянути часткові коефіцієнти кореляції (Partial Cor.) між змінними (рис. 14.7). Часткова кореляція характеризує зв’язки між двома змінними, коли одна або більше з них мають постійне значення. Часткові коефіцієнти кореляції, як і парні, можуть приймати значення від -1 до +1.

|
| Рис. 14.7. Результати розрахунку приватних коефіцієнтів кореляції |
Сильні взаємозв’язки між незалежними змінними у нашому рівнянні утрудняє аналіз впливу окремих факторів на залежну змінну. В ідеальній регресійній моделі незалежні змінні взагалі не корелюють одна з однією. Однак у моделях, розроблювальних для природних об'єктів, сильна кореляція змінних є досить частим явищем. Це приводить до збільшення похибки рівняння, зменшення точності оцінювання, знижується ефективність використання регресійної моделі. Саме тому вибір незалежних змінних, що включають у регресійну модель, повинен бути дуже ретельним.
Кнопка Redundancy призначена для пошуку викидів. Викиди - це залишки, які значно перевершують за абсолютним значенням інші. Викиди показують дослідні дані, які є не типовими стосовно інших даних, і вимагають з'ясування причин їхнього виникнення. Викиди повинні виключатися з вибірки, якщо вони викликані помилками реєстрації, або вимірів. Для виділення наявних у регресійних залишках викидів є ряд показників:
Показник Кука (Cook's Distance) приймає тільки позитивне значення й показує відстань між коефіцієнтами рівняння регресії після виключення з аналізу i-того показника.
Відстань Махаланобіса (Mahalns. Distance) показує наскільки кожний показник в р-мірному просторі незалежних змінних відхиляється від центра статистичної сукупності.
Уважний аналіз залишків дозволяє оцінити адекватність моделі. Залишки повинні бути нормально розподілені, із середнім значенням рівним нулю й постійною (незалежно від величин залежної й незалежної змінних) дисперсією. Модель повинна бути адекватна на всіх відрізках інтервалу зміни залежної змінної.
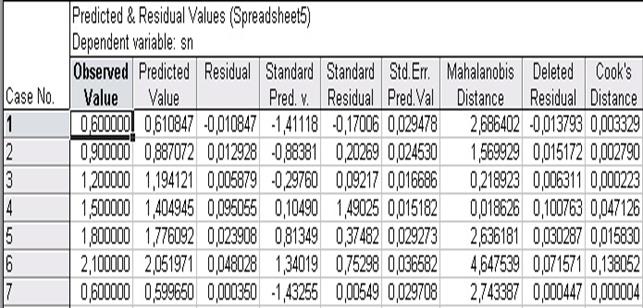
Перегляд величин залишків і спеціальних критеріїв їх оцінки здійснюється за допомогою вкладки Residuals/assumptions/prediction кнопка Perform residual analysis. Для нашого прикладу фрагмент вікна із цими результатами наведений на рис. 14.8.
|
| Рис.14.8. Вікно зі значеннями залишків (Residuals), показниками Кука (Cook's Distance), відстані Махаланобіса (Mahalns. Distance), дослідними (Observed Value) і передбаченими по рівнянню (Predictd Value) значеннями залежної змінної |
Дата добавления: 2015-04-25; просмотров: 1305;
