Дисперсійний аналіз
Дисперсійний аналіз проводиться у прикладній програмі, розглянутій вище, тому процеси створювання файла і заповнення таблиці ми опускаємо. Унаслідок проведеної роботи отримуємо робочий лист, наведений на рис. 13.7.
Результати досліджень на листу розташовані так, що під кожен фактор досліду та ознаку, що вивчається, відводиться окремий стовпчик (Var), а під варіанти
досліду — рядки (Case), тобто  серед досліджуваних факторів, що впливають на врожайність цукрових буряків, є добрива, ЧС гібриди і строки сівби.
серед досліджуваних факторів, що впливають на врожайність цукрових буряків, є добрива, ЧС гібриди і строки сівби.
Для проведення дисперсійного аналізу у верх-ньому меню обираємо пу-нкт “Statistics”, а в ньому – пункт “ANOVA” (рис. 13.8).

 Після цього на екрані з’являється вікно, у якому надається можливість обрати тип дисперсійного аналізу – однофакторний – One-way ANOVA, аналіз головних ефектів — Main effects ANOVA, факторіальний – Factorial ANOVA та з повторними вимірюваннями Repeated measures ANOVA .
Після цього на екрані з’являється вікно, у якому надається можливість обрати тип дисперсійного аналізу – однофакторний – One-way ANOVA, аналіз головних ефектів — Main effects ANOVA, факторіальний – Factorial ANOVA та з повторними вимірюваннями Repeated measures ANOVA .
Ми обираємо факто-ріальний аналіз, який доз-воляє розрахувати дисперсії всіх факторів та всіх їх взаємодій. Натискаємо кнопку „ОК” і переходи-мо до наступного вікна.
 Пакет не обов’язково використовує для аналізу всю інформацію, що знаходиться у файлі даних, тому у вікнах, що наведені на рис. 13.9 і 13.10, надається можливість вибрати ті змінні й фактори, з якими ми будемо працювати.
Пакет не обов’язково використовує для аналізу всю інформацію, що знаходиться у файлі даних, тому у вікнах, що наведені на рис. 13.9 і 13.10, надається можливість вибрати ті змінні й фактори, з якими ми будемо працювати.
Для того, щоб їх обрати, слід натиснути кнопку „Variables” (Змінні). З’явиться вікно „Вибір залежних змінних та категоріальних предикторів (факторів)” (рис. 13.11).

 У лівій частині вікна обираємо залежні змінні (у нашому випадку – урожайність), а у правій – фактори досліду (у нашому випадку – добрива, ЧС гібриди та строки сівби). Натискаємо „ОК”
У лівій частині вікна обираємо залежні змінні (у нашому випадку – урожайність), а у правій – фактори досліду (у нашому випадку – добрива, ЧС гібриди та строки сівби). Натискаємо „ОК”
|
Вивчаємо попереднє вікно (рис. 13.9), в якому надписи напроти кнопок “Dependent variables” (Залежні показники) та “Categorical factors”  (Категорії факторів) змінилися і відображають
(Категорії факторів) змінилися і відображають  тепер обрані нами (рис. 13.10).
тепер обрані нами (рис. 13.10).
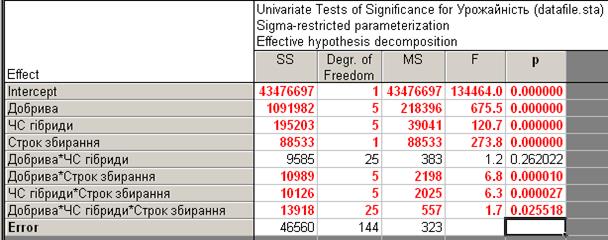
Кнопка „Factor codes” (Коди факторів) дозволяє виключити з аналізу певні градації факторів. Оскільки ми залучаємо до аналізу всі градації, наявні у файлі даних, цю кнопку залишаємо без уваги. Кнопка “Between effects” (Ефекти між) служить для корекції ефектів, які будуть проаналізовані. Якщо залишити цю кнопку без уваги, будуть проаналізовані всі ефекти і всі їх можливі комбінації. Обравши потрібні опції, натискаємо „ОК”, в новому вікні після натискання кнопки “All effects” (рис. 13.12) з’являється вікно з таблицею результатів дисперсійного аналізу (рис. 13.13).
|
Тут виділені ефекти, що є достовірними на 5 %-му, а де р < 0.01, то й на 1 %-му рівні значущості. У нашому прикладі такими є всі фактори, крім взаємодії ЧС гібриди * Добрива.
На цьому дисперсійний аналіз завершується.
Оскільки у нас виявлені достовірні різниці за рядом факторів і їх взаємодій, то виникає інтерес до виявлення варіантів з такими різницями. Мова йде про класичне виділення варіантів з істотними різницями до контролю або між окремими варіантами.
З вікна (рис. 13.12) є можливість побудувати й графіки, для чого треба натиснути кнопку “All effects/Graphs”, і з’явиться таблиця дисперсійного аналізу з можливістю вибрати вид ефекту та побудувати для нього графік (рис. 13.14).
|
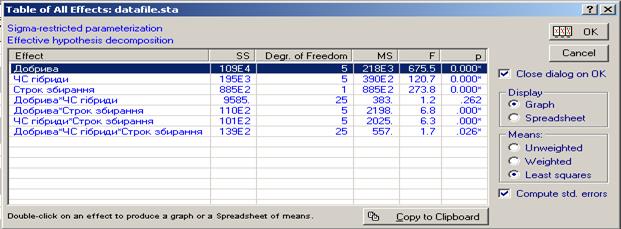
Наприклад, якщо вибрати ефект взаємодії Добрива*Строки збирання, спочатку з’являється вікно (рис. 13.15), що при виборі головних ефектів не з’являється, в якому можна обрати, який з ефектів взаємодії буде подано на осі Х, а який – лініями різного кольору.
|

Як наслідок отримаємо графік (рис. 13.16), на якому показано вплив ЧС гібридів та строків збирання на врожайність цукрових буряків.
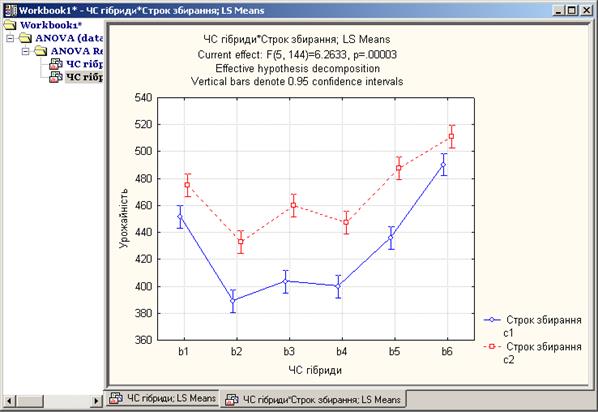
Рис. 13.16. Вікно з побудованим графіком
Слід зауважити, що пакет Statistica 6.0 має потужну систему побудови різноманітних графіків. Для зручного розміщення графіка у студентських наукових роботах, звітах або дисертаціях є можливість змінити його вигляд, надписи осей, шрифтів та ін.
Важливим атрибутом таблиць і графіків є статистичні показники оцінки результатів досліджень. Найбільш часто науковці використовують одноранговий критерій найменшої істотної різниці (НІР), основна перевага якого є легкість його обчислення, але він добре підходить для порівняння варіантів з контролем і має певні недоліки при порівнянні варіантів один з одним.
Повернувшись до вікна результатів (рис. 13.12), натискаємо кнопку “More results” (Більше результатів), а у вікні, що розвернулося, — вкладку “Post-hoc” (Оцінка показників, рис. 13.17). Розглянемо значення цієї форми.
Effect — вибір фактора або взаємодії, для яких проводитимуться розрахунки — Добрива*ЧС гібриди*Строк збирання.
Dependent variables — кнопка для визначення залежного або залежних показників.
Display — показник, що виводиться на екран.
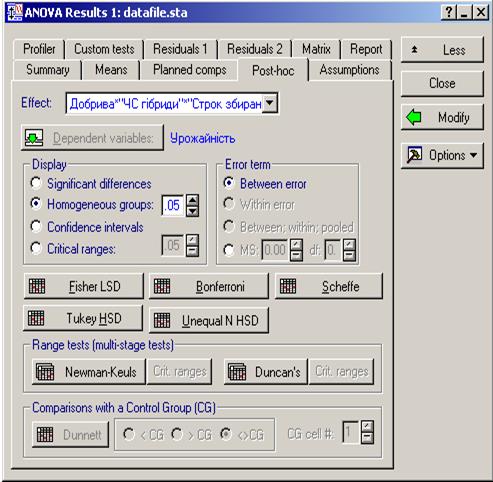
Рис. 13.17. Форма для розрахунку істотності різниць між варіантами
Significant differences — достовірні різниці — виведення на екран квадратної матриці достовірних різниць (жирні цифри). І навпаки, немає істотної різниці між гібридами b1 та b5 і між гібридами b3 та b4, коли цифри звичайні (рис. 13.18).
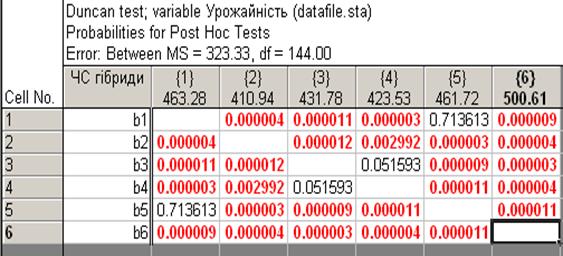
Рис. 13.18. Жирним шрифтом подано варіанти
з істотними різницями між гібридами
Homogeneous groups — видає середні значення у вигляді ранжованих гомогенних груп за рівнем значущості. Так, дані, що були наведені в табл. 32 і 33, за істотністю різниць між гібридами теж попадають в однакові групи (гібриди b1 та b5 — до гомогенної групи 2, b3 та b4 - до групи 3).
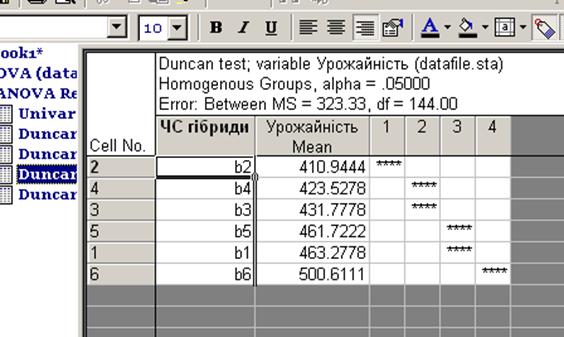
Рис. 13.19. Гомогенні групи за істотністю різниць між гібридами
Цей спосіб представлення даних, на нашу думку, є найбільш компактним і наочним.
Confidence intervals — видає довірчі інтервали. Найчастіше характеризують достовірний інтервал за Фішером (Fisher LSDФішер НІР,рис. 12.20); наводять абсолютні різниці між варіантами та межі довірчого інтервалу різниць між ними. Невиділеними залишилися варіанти з різницями менше за НІР05, тобто, як і вище, немає істотної різниці між гібридами b1 і b5 та b3 і b4.
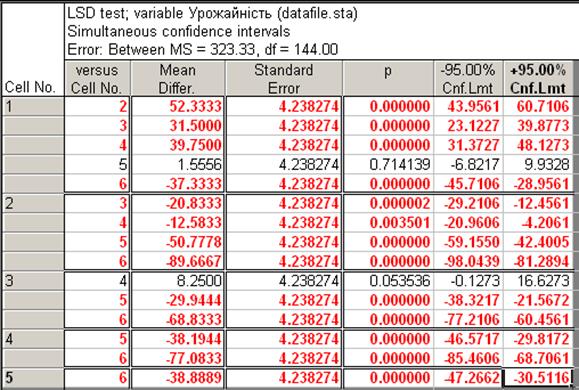
Рис. 13.20. Жирним шрифтом наведено істотні різниці між гібридами
на 5 %-му рівні значущості або 95 % рівні ймовірності
Critical ranges — критичні межі — показують значення істотних різниць за критеріями Дункана або Ньюмена-К’юлза. Вони дозволяють встановити істотність різниць між членами ранжованого ряду на певному рівні значущості (у нашому випадку 5 %-му). Step 1 (крок 1) дозволяє встановити істотну різницю між сусідніми членами ранжованого ряду (тобто віддалених між собою на два місця); він дорівнює найменшій істотній різниці (НІР). Step 2 — для членів ряду віддалених на три місця (1 та 3, 2 та 4) і так далі (рис. 12.21).
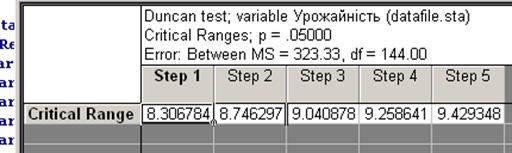
Рис. 12.21. Значення НІР05, за критерієм Дункана
У цій же формі є кнопки для оцінки результатів за різними критеріями.
Слід звернути увагу на можливість оцінки взаємодій між факторами та їх інтерпретацію. Наприклад, на рис. 12.22 наведено гомогенні групи за ефектом взаємодії ЧС гібриди х Строки збирання, на підставі яких можна зробити висновок, що строки збирання впливають на врожайність усіх досліджуваних гібридів.
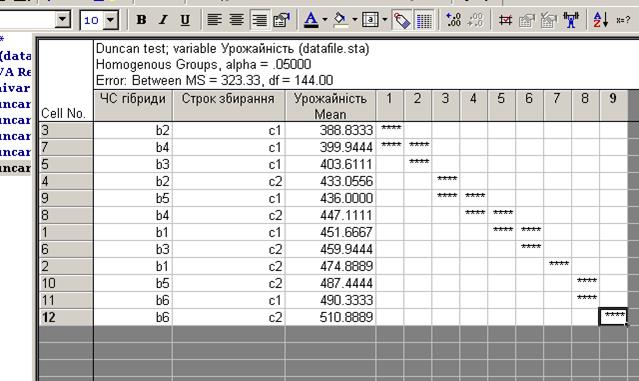
Рис. 13.22. Гомогенні групи для взаємодії ЧС гібриди*Строки збирання
Отже, використання прикладного пакета Statistica 6.0 дозволяє зосередити увагу не на обчисленнях за складними формулами, а, знаючи лише основні принципи статистичного аналізу, глибоко аналізувати складні біологічні процеси і їх взаємодії.
При інтерпретації результатів статистичної обробки за допомогою гомогенних груп, недоліком є наскрізне ранжування ряду варіантів за величиною досліджуваної ознаки, що ускладнює розуміння застосованих градацій факторів. Тому кожній гомогенній групі надають латинську букву і в кінцевій таблиці, де результати показані згідно градацій факторів, напроти варіанту ставлять букви, які відповідають гомогенним групам, до яких належить цей варіант.
Таким чином, при попарному порівнянні варіантів, якщо біля них немає однакової букви, то різниця між ними достовірна на прийнятому рівні значущості.
Наприклад, результати рис. 13.22 можна інтерпретувати так, як наведено в табл. 13.2.
Таблиця 13.2
Урожайність цукрових буряків залежно від строків збирання ЧС-гібриду
| ЧС гібриди | Строки збирання | Код | Урожайність, ц/га | Порівняння за кодами |
| B1 | C1 | a | ef | |
| C2 | b | g | ||
| B2 | C1 | c | a | |
| C2 | d | c | ||
| B3 | C1 | e | b | |
| C2 | f | f | ||
| B4 | C1 | g | ab | |
| C2 | h | de | ||
| B5 | C1 | i | cd | |
| C2 | j | h | ||
| B6 | C1 | k | h | |
| C2 | l | i |
За цим же принципом можемо визначати й інші взаємодії факторів досліду навіть з більш високими рівнями взаємодій факторів.
13.3. Кореляція і регресія
Кореляційною є залежність, коли зі збільшенням середньої величини першої ознаки збільшується середня величина другої, або, навпаки, зі збільшенням середньої величини першої ознаки - друга зменшується. У першому випадку кореляція є пряма або позитивна, у другому - оберненою або від’ємною.
На відміну від функціональної залежності при кореляції одному значенню першої ознаки відповідає не одна, а кілька значень другої ознаки. Кореляція є парна, якщо досліджується зв’язок між двома ознаками і множинною, коли на величину однієї результативної ознаки впливають декілька факторіальних.
Парна лінійна кореляція між ознаками х та у позначається коефіцієнтом (r) і розраховується за формулою:
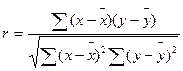 =
= 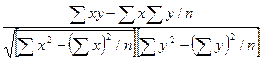 .
.
Значення коефіцієнта кореляції лежить у межах від +1 до -1. Вважають, що при r<0,3 кореляційна залежність між ознаками слабка, r= 0,3-0,7 – середня і r>0,7 – сильна.
Квадрат коефіцієнта кореляції (r2) називається коефіцієнтом детермінації і позначається dyx.. Він показує частку або відсоток тих вимірювань, які в даному явищі залежать від фактора, що вивчається.
Критерій істотності коефіцієнта кореляції розраховують за формулою:
tr = r/Sr.
Якщо tr > t ф,, то кореляційний зв’язок істотний, а коли tr < tф — неістотний. Теоретичне значення критерію t знаходять по таблиці І додатків при ступені волі n – 2. Регресія показує кількісну зміну на одиницю виміру результативної (залежної) ознаки (функції У) при зміні факторіальної ознаки (аргументу Х). Вона теж є простою, якщо функція досліджується залежно від одного аргументу (y = f(x)), і множинною - від двох чи більше аргументів (y = f(k, z, v)).
Залежність функції від аргументу при лінійній регресії виражається коефіцієнтом регресії (byx або bxy), який показує, в якому напрямі і на яку величину змінюється одна ознака при зміні іншої на одиницю виміру:
byx = rσy /σx, або bxy = r σx /σy.
Коефіцієнт регресії має знак коефіцієнта кореляції. Добуток коефіцієнтів регресії дорівнює квадрату коефіцієнтів кореляції (коефіцієнту детермінації):
byx bxy = r2.
Кореляція може бути зображена графічно у вигляді лінії регресії. Для побудови графіка по осі абсцис відкладають значення ознаки х, а по осі ординат - значення ознаки у; кожне спостереження над двома змінними відмічають точкою з координатами (х, у).
Завдання. Визначить коефіцієнт прямолінійної кореляції та складіть
рівняння регресії про залежність між кількісними ознаками рослин гороху. Зробіть висновок і графічну інтерпретацію регресивної залежності.
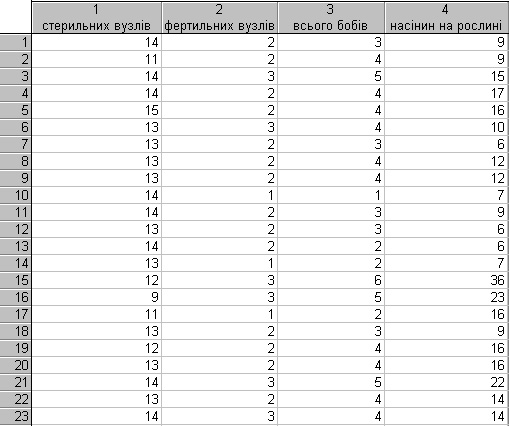
Вихідні дані для визначення тісноти взаємозв'язків між кількісними ознаками рослин гороху представлені на рис. 13.23.
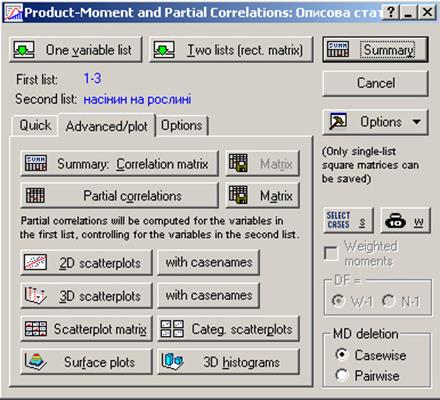
У стартовому вікні цієї процедури "Product-Moment and Partial Correlation" (рис.12.24) для розрахунку квадратної матриці використовується кнопка One variable list, а для обчислення прямокутної матриці – Two lists (rect. matrix).
|
| Рис. 13.23. Вікно файлу вихідних даних |
|
| Рис. 13.24. Вікно Product-Moment and Partial Correlation |
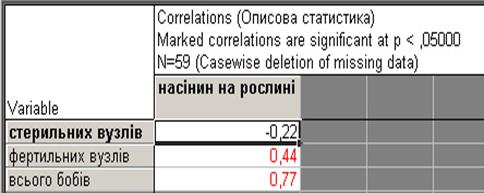
У списку змінних вибирають змінні, між якими будуть розраховані парні коефіцієнти кореляції Пірсона. Після натискання на кнопку Summary на екрані з'явиться кореляційна матриця (рис. 13.25).
|
| Рис. 13.25. Кореляційна матриця |
Процедура Correlation matrices одразу ж дає можливість перевірити вірогідність розрахованих коефіцієнтів кореляції. Значення коефіцієнта кореляції може бути високим, але не достовірним, випадковим. Щоб побачити ймовірність нульової гіпотези (p), що свідчить про те, що коефіцієнт кореляції дорівнює 0, потрібно у вкладці Options опції Display вікна Product-Moment and Partial Correlation (рис. 13.26) установити перемикач на другий рядок Display r, p-levels, and N’s.
|
| Рис. 13.26. Вибір додаткових параметрів |
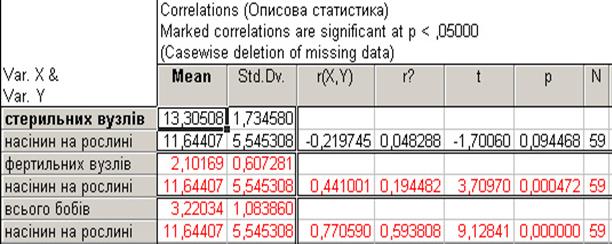
Але, навіть якщо цього не робити й залишити перемикач у першому положенні Display simple matrix (highlight p’s), статистично значимі на 5 %-му рівні коефіцієнти кореляції будуть виділені в кореляційній матриці червоним кольором. Третє положення перемикача опції Display — Detail table of results дозволяє переглянути результати кореляційного аналізу в деталях (рис. 13.27). Прапорець опції MD deletion Casewise установлюється для виключення з обробки всього рядка файла даних, у якому є хоча б одне пропущене значення.
|
| Рис. 13.27. Варіант детального перегляду результатів кореляційного аналізу |
За допомогою Correlation matrices можна встановити тісноту лінійного зв’язку між досліджуваними ознаками, а також перевірити вірогідність розрахованих коефіцієнтів кореляції.
На рис. 13.27 представлені такі показники:
Mean — середня арифметична; Середнє значення випадкової величини є найбільш типовим, найбільш імовірним значенням, своєрідним центром, навколо якого розкидані всі значення ознаки;
Standard Deviation — стандартне відхилення; Стандартне відхилення (або середнє квадратичне відхилення) є мірою мінливості (варіації) ознаки. Воно показує, на яку величину в середньому відхиляються показники від середнього значення ознаки. За умов нормального розподілу 68 % усіх показників лежить в інтервалі ± одного відхилення від середнього, 95 % — ± двох стандартних відхилень від середнього й 99,7 % усіх показників — в інтервалі ± три стандартних відхилення від середнього.
r (X Y) – коефіцієнт кореляції;
(r2) – коефіцієнт детермінації.
Коефіцієнт апроксимації виражає частку варіації залежної змінної, визначену коефіцієнтом кореляції, тобто на скільки точно рівняння описує дослідні дані;
Р – рівень значущості. Якщо значення р не перевищує 5-% рівня значу-щості, то такий коефіцієнт кореляції можна вважати достовірним на 5 %-му рівні значущості;
t – критерій Ст’юдента;
N – загальна кількість спостережень;
Усього бобів = 1,4666 + , 15062 * насінин на рослині
Correlation: r = , 77059
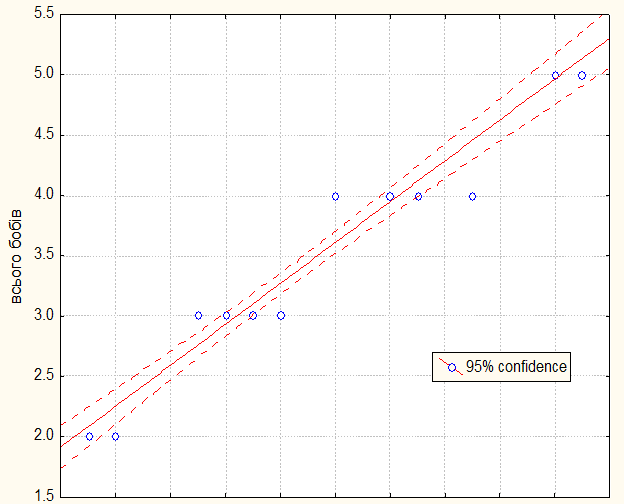
Насінин на рослині
Рис. 13.28 Графік – Scatterplot: насінин на рослині vs. усього бобів (Casewise MD deletion)
Висновок. Між кількістю бобів і кількістю насінин на рослині встановлена тісна позитивна кореляційна залежність (r=0,77). Лінія регресії і ії довірчий інтервал на 5 %-му рівні значущості ведені на рис. 13.28.
Дата добавления: 2015-04-25; просмотров: 2254;
