Gravitational Potential Energy

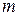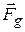We first consider a particle with mass moving vertically along a axis (the positive direction is upward). As the particle moves from pointy to pointy, the gravitational force does work on it. To find the corresponding change in the gravitational potential energy of the particle-Earth system, we use Eq. 8-6 with two changes: (1) We integrate along the axis instead of the axis, because the gravitational force acts vertically (2) We substitute for the force symbol , because 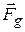has the magnitude and is directed down the axis. We then have

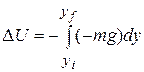
which yields

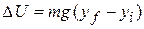(8-7)

Only changes 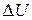ingravitational potential energy (or any other type of potential energy) are physically meaningful. However, to simplify a calculation or a discussion, we sometimes would like to say that a certain gravitational potential value U is associated with a certain particle-Earth system when the particle is at a certain height y. To do so, we rewrite Eq. 8-7 as

. (8-8)

Then we take to be the gravitational potential energy of the system when it is ina reference configurationin which the particle is at a reference point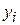. Usually we take and . Doing this changes Eq. 8-8 to

(gravitational potential energy). (8-9)

This equation tells us:

► The gravitational potential energy associated with a particle-Earth system depends only on the vertical position (or height) of the particle relative to the reference position 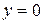, not on the horizontal position.