Finding the Force Analytically

Equation 8-6 tells us how to find the change 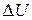in potential energy between two points in a one-dimensional situation if we know the force 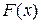. Now we want to go the other way; that is, we know the potential energy function 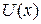and want to find the force.

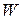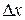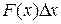For one-dimensional motion, the work done by a force that acts on a particle as the particle moves through a distance is . We can then write Eq. 8-1 as

.

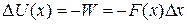Solving for 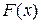and passing to the differential limit yield

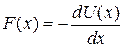(one-dimensional motion).-- (8-20)

-which is the relation we sought.

We can check this result by putting 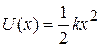, which is the elastic potential energy function for a spring force. Equation 8-20 then yields, as expected, 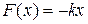, which is Hooke's law. Similarly, we can substitute 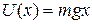, which is the gravitational potential energy function for a particle-Earth system, with a particle of mass m at height x above Earth's surface. Equation 8-20 then yields 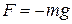, which is the gravitational force on the particle.