Equilibrium Points
Figure 8-10c shows three different values for 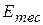 superposed on the plot of the same potential energy function
superposed on the plot of the same potential energy function 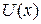 . Let us see how they would change the situation. If
. Let us see how they would change the situation. If 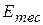 = 4.0 J (purple line), the turning point shifts from
= 4.0 J (purple line), the turning point shifts from 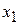 to a point between
to a point between 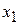 and x2. Also, at any point to the right of
and x2. Also, at any point to the right of  , the system's mechanical energy is equal to its potential energy; thus, the particle has no kinetic energy and (by Eq. 8-20) no force acts on it, and so it must be stationary. A particle at such a position is said to be in neutral equilibrium.(A marble placed on a horizontal tabletop is in that state.)
, the system's mechanical energy is equal to its potential energy; thus, the particle has no kinetic energy and (by Eq. 8-20) no force acts on it, and so it must be stationary. A particle at such a position is said to be in neutral equilibrium.(A marble placed on a horizontal tabletop is in that state.)
If 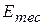 = 3.0 J (pink line), there are two turning points: One is between
= 3.0 J (pink line), there are two turning points: One is between 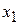 and
and 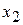 , and the other is between
, and the other is between 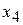 and
and  . In addition,
. In addition, 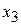 is a point at which
is a point at which  . If the particle is located exactly there, the force on it is also zero, and the particle remains stationary. However, if it is displaced even slightly in either direction, a nonzero force pushes it farther in the same direction, and the particle continues to move. A particle at such a position is said to be in unstable equilibrium.(A marble balanced on top of a bowling ball is an example.)
. If the particle is located exactly there, the force on it is also zero, and the particle remains stationary. However, if it is displaced even slightly in either direction, a nonzero force pushes it farther in the same direction, and the particle continues to move. A particle at such a position is said to be in unstable equilibrium.(A marble balanced on top of a bowling ball is an example.)
Next consider the particle's behavior if 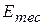 = 1.0 J (green line). If we place it at
= 1.0 J (green line). If we place it at 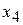 , it is stuck there. It cannot move left or right on its own because to do so would require a negative kinetic energy. If we push it slightly left or right, a restoring force appears that moves it back to
, it is stuck there. It cannot move left or right on its own because to do so would require a negative kinetic energy. If we push it slightly left or right, a restoring force appears that moves it back to 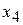 : A particle at such a position is said to be in stable equilibrium.(A marble placed at the bottom of a hemispherical bowl is an example.) If we place the particle in the cuplike potential well centered at
: A particle at such a position is said to be in stable equilibrium.(A marble placed at the bottom of a hemispherical bowl is an example.) If we place the particle in the cuplike potential well centered at 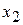 , it is between two turning points. It can still move somewhat, but only partway to
, it is between two turning points. It can still move somewhat, but only partway to 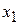 or
or 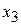 .
.
Дата добавления: 2015-06-17; просмотров: 803;
