Friction Involved

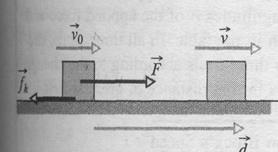
We next consider the example in Fig. 8-13a. A constant horizontal force pulls a block along an axis and through a displacement of magnitude 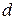, increasing the block's velocity from 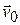to 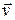. During the motion, a constant kinetic frictional force 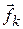from the floor acts on the block. Let us first choose the block as our system and apply Newton's second law to it. We can write that law for components along the axis ( )as

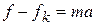
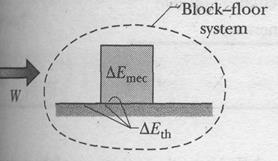
Because the forces are constant, the acceleration 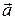is also constant. Thus, we can use Eq. 2-16 to write

.

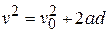Solving this equation for 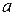, substituting the result into Eq. 8-25, and rearranging then give us

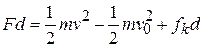
because for the block,

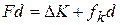
In a more general situation (say, one in which the block is moving up a ramp), there can be a change in potential energy. To include such a possible change, we generalize Eq. 8-27 by writing

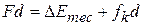8-28

By experiment we find that the block and the portion of the floor along which it slides become warmer as the block slides. As we shall discuss in Chapter 19, the temperature of an object is related to the object's thermal energy 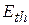(the energy associated with the random motion of the atoms and molecules in the object). Here, the thermal energy of the block and floor increase because (1) there is friction between them and (2) there is sliding. Recall that friction is due to the cold-welding between two surfaces. As the block slides over the floor, the sliding causes repeated tearing and reforming of the welds between the block and the floor, which makes the block and floor warmer. Thus, the sliding increases their thermal energy .

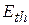Through experiment, we find that the increase 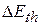in thermal energy is equal to the product of the magnitudes 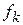and :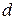

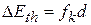(-increase in thermal energy by sliding). 8-29

Thus, we can rewrite Eq. 8-28 as

8-30

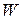is the work done by the external force (the energy transferred by the force), but on which system is the work done (where are the energy transfers made)? To answer, we check to see which energies change. The block's mechanical energy changes, and the thermal energies of the block and floor also change. Therefore, the work done by force F is done on the block-floor system. That work is

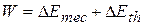(8-31)

This equation, which is represented in Fig. 8-13b, is the energy statement for the work done on a system by an external force when friction is involved.

8-7 Conservation of Energy

We now have discussed several situations in which energy is transferred to or from objects and systems, much like money is transferred between accounts. In each situation we assume that the energy that was involved could always be accounted for; that is, energy could not magically appear or disappear. In more formal language, we assumed (correctly) that energy obeys a law called the law of conservation of energy,which is concerned with the totalenergy of a system. That total is the sum of the system's mechanical energy, thermal energy, and any form of internal energy in addition to thermal energy. (We have not yet discussed other forms of internal energy.) The law states that

> The total energy of a system can change only by amounts of energy that are transferred to or from the system.

The only type of energy transfer that we have considered is work 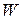done on a system. Thus, for us at this point, this law states that

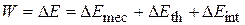
where 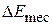is any change in the mechanical energy of the system, 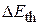is any change in the thermal energy of the system, and is any change in any other form of internal energy of the system. Included in 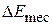are changes 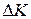in kinetic energy and changes 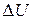in potential energy (elastic, gravitational, or any other form we might find).

This law of conservation of energy is not something we have derived from basic physics principles. Rather, it is a law based on countless experiments. Scientists and engineers have never found an exception to it.