Sample Problem 8-7

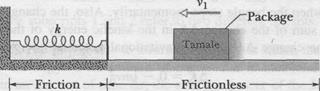
In Fig. 8-15, a 2.0 kg package of tamale slides along a floor with speed v₁ = 4.0 m/s. It then runs into and compresses a spring, until the package momentarily stops. Its path to the initially relaxed spring is frictionless, but as it compresses the spring, a kinetic frictional force from the floor, of magnitude 15 N, acts on it. The spring constant is 10,000 N/m. By what distance d is the spring compressed when the package stops?

SOLUTION: A starting Key Idea is to examine all the forces acting on the package, and then to determine whether we have an isolated system or a system on which an external force is doing work.

Forces: The normal force on the package from the floor does no work on the package, because its direction is always perpendicular to that of the package's displacement. For the same reason, the gravitational force on the package does no work. As the spring is compressed, however, a spring force does work on the package, transferring energy to elastic potential energy of the spring. The spring force also pushes against a rigid wall. Because there is friction between the package and the floor, the sliding of the package across the floor increases their thermal energies.

System: The package-spring-floor-wall system includes all these forces and energy transfers in one isolated system. Therefore, a second Key Idea is that, because the system is isolated, its total energy cannot change. We can then apply the law of conservation of energy in the form of Eq. 8-35 to the system:

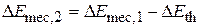(8-38)

Let subscript 1 correspond to the initial state of the sliding package, and subscript 2 correspond to the state in which the package is momentarily stopped and the spring is compressed by distance 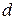. For both states the mechanical energy of the system is the sum of the package's kinetic energy ( )and the spring's potential energy ( ). For state 1, 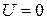(because the spring is not compressed), and the package's speed is 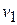|. Thus, we have

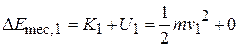
For state 2, (because the package is stopped), and the compression distance is 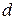. Therefore, we have

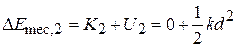
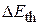Finally, by Eq. 8-29, we can substitute for the change in the thermal energy of the package and the floor. We can now re­write Eq. 8-38 as

.

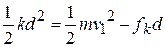Rearranging and substituting known data give us

.

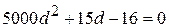Solving this quadratic equation yields

d = 0.055 m = 5.5 cm.

(Answer)

EXAMPLE 7—5 A man holds a ball of mass 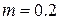kg at rest in his hand. He then throws the ball vertically upward. In this process, his hand moves up 0.5 m before the ball leaves his hand with an upward velocity of 20 m/s. Discuss the motion of the ball from the work-energy standpoint, assuming 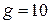m/s².

SOLUTION First, consider the throwing process. Take the reference level ( 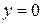) at the initial position of the ball. Then 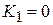, 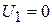. Take point 2 at the point where the ball leaves the thrower's hand. Then

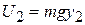= (0.2 kg)(10 m/s²)(0.5 m) = 1.0 J,

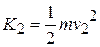= 1(0.2 kg)(20 m/s)² = 40 J.

Let 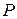represent the upward force exerted on the ball by the man in the throwing process. The work 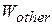is then the work done by this force and is equal to the sum of the changes in kinetic and potential energy of the ball. The kinetic energy of the ball increases by 40 J and its potential energy by 1 j. The work 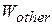done by the upward force 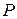is therefore 41 J.

If the force 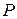is constant, the work done by this force is given by

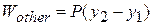
and the force 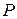is then

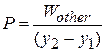
However, the work done by the force 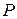is 41 J whether the force is constant or not.

Now consider the flight of the ball after it leaves the thrower's hand. In the absence of air resistance, the only force of the ball is then its weight 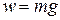. Hence the total mechanical energy of the ball remains constant. The calculations are simpler if we take a new reference level at the point where the ball leaves the thrower's hand. Calling this point 1, we have

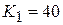J, ,

,

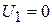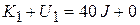and the total mechanical energy at any point in the path is 40 J.

Suppose we want to find the speed of the ball at a height of 15 m above the reference level. Its potential energy at this elevation is

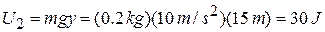
Therefore the kinetic energy at this point is 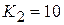J, and the speed 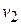at this point is given by

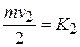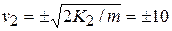, m/s.

The significance of the ± sign is that the ball passes this point twice, once on the way up and again on the way down. Its potential energy at this point is the same whether it is moving up or down. Hence its kinetic energy is the same and its speed is the same. The algebraic sign of the velocity is + when the ball is moving up and — when it is moving down.

Next, let us find the highest point the ball reaches. At this point 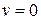and . Therefore at this point ], and the maximum height 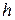of the ball above the thrower's hand is given by

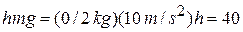J

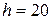And m.

Finally, suppose we are asked to find the ball's speed at a point 30 m above the reference level. The potential energy at this point would be 60 J. But the total energy is only 40 J, so the ball can never reach a height of 30 m.

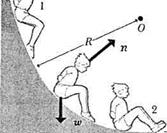
EXAMPLE 7-6 A child slides down a curved playground slide that is one quadrant of a circle of radius 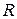, as in Fig. 7-9. If he starts from rest and there is no friction, find his speed at the bottom of the slide. (The motion of this child is exactly the same as that of a child on a swing of length 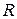, with the other end held at point O.)

SOLUTION We cannot use the equations of motion with constant acceleration because the acceleration decreases during the motion. (The slope angle of the slide becomes smaller and smaller as the body descends.) If there is no friction, however, the only force on the child other than his weight is the normal force 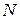exerted on him by the slide. The work done by this force is zero because at each point it is perpendicular to the small element of displacement near that point. Thus 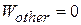and mechanical energy is conserved. Take point 1 at the starting point and point 2 at the bottom of the slide. Take the reference level at point 2. Then 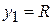, , 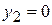and

,

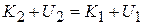
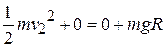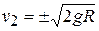
The speed is therefore the same as if the child had fallen vertically through a height 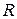. (What is now the significance of the ± sign?) As a numerical example, let 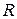= 3.00 m. Then

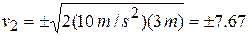m/s.

EXAMPLE 7—7 Suppose a child of mass 25.0 kg slides down a slide of radius R = 3.00 m, like that in Fig. 7-9, but his speed at the bottom is only 3.00 m-s^-1. What work was done by the frictional force acting on the child?

SOLUTION In this case,

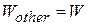
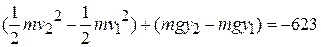J

The frictional work was therefore -623 J, and the total mechanical energy decreased by 623 J. The mechanical energy of a body is not conserved when friction forces act on it.

EXAMPLE 7—9 A child of weight sits on a swing of length 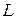, as shown in Fig. 7—11. A variable horizontal force 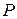that starts at zero and gradually increases is used to pull the child very slowly (so the kinetic energy is negligibly small) until the swing makes an angle 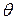with the vertical. Calculate the work done by the force .

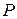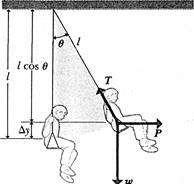
SOLUTION The sum of the works done by all the forces other than the gravitational force must equal the change of total energy, that is, the change of

kinetic energy plus the change of gravitational potential energy. Hence

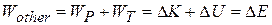
Since 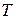is perpendicular to the path at its point of application, 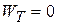; and since the swing was pulled very slowly at all times, the change of kinetic energy is also zero. Hence

,

where 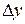is the distance that the child has been raised. From Fig. 7-11, 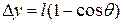.Therefore

.

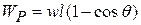Note that this result agrees with that obtained in Example 7-3, where W_P was calculated directly.

Find the work done in moving a particleali

Q. 1.13. Find the work done in moving a particle alone a vector 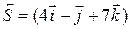meters, if the applied force is 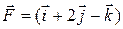Newton.

Solution.

Here, 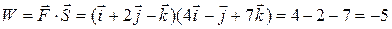J

Derive an expression for the gravitational potential energy of a body lying at a height 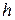( 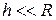), radius of earth) above the surface of earth.

Define kinetic energy. Derive an expression for the kinetic energy of a body moving with a uniform velocity.

Derive the expression for the kinetic energy of a mass m moving with a velocity v. Define SI unit of energy.

State and prove work-energy theorem.

Define work, power and energy giving their units in SI. Prove that work done by constant force is equal to the total change in kinetic energy of the body, whose initial and final velocities are и and v respectively.

Explain the meaning of the term work. Calculate the work done by a constant force. Is work a scalar or a vector quantity ?

Explain the term work. Show that work done is equal to dot product of force and displacement.

What is meant by positive work, negative work and zero

work? Give one example of each.

Define work. What is SI unit of work ? What is meant by positive work, negative work and zero work ?

Explain, how can we find the work done by a variable force.

What is a conservative force ? Explain its various properties.

Define power. What is SI unit of power ? Prove that instantaneous power is given by the scalar product of force and velocity.

Define and explain the terms : work, energy and power. State their SI units.

Define energy and power. What are their units in SI

system?

Define work and power. State their SI units.

Show that the total mechanical energy of a body f ailing freely under gravity is conserved.

What are elastic and inelastic collisions? Give examples.

Type A. On Work done

1. What is the work done by a man in carrying a suitcase weighing 30 kg over his head, when he travels a distance of 10 m in the (/) vertical direction, (ii) horizontal direction ?

[Ans. (z) 2,940 J; (ii) zero]

2. Find the work done, if a weight of 25 kg is lifted through a vertical height of 2 m from the ground and also if it is raised to same place by pushing up an inclined plane making an angle of 30° with the ground. Neglect friction.

[Ans. 490 J; 490 J]

3. A man weighing 50 kg climbs 10 m. Calculate the work
done by gravity.[Ans. - 4,900 J]

4. A particle is displaced through 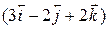meters under the influence of a force 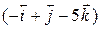newton. Calculate the work done.

( [Ans. - 15 J]

5. A particle moves from a point 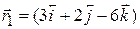to position 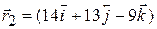under the action of a force 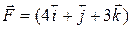newton. If the displacement between two points is in meters, calculate the work done.

[Ans. 46 J]