Isolated System

If a system is isolated from its environment, then there can be no energy transfers to or from it. For that case, the law of conservation of energy states:

The total energy of an isolated system cannot change.

Many energy transfers may be going on within an isolated system, between, say, kinetic energy and a potential energy or kinetic energy and thermal energy. However, the total of all the forms of energy in the system cannot change.

We can use the rock climber in Fig. 8-14 as an example, approximating her, her gear, and Earth as an isolated system. As she rappels down the rock face, changing the configuration of the system, she needs to control the transfer of energy from the gravitational potential energy of the system. (That energy cannot just disappear.) Some of it is transferred to her kinetic energy. However, she obviously does not want very much transferred to that form or she will be moving too quickly, so she has wrapped the rope around metal rings to produce friction between the rope and the rings as she moves down. The sliding of the rings on the rope then transfers the gravitational potential energy of the system to thermal energy of the rings and rope in a way that she can control. The total energy of the climber-gear-Earth system (the total of its gravitational potential energy, kinetic energy, and thermal energy) does not change during her descent.

For an isolated system, the law of conservation of energy can be written in two ways. First, by setting 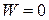in Eq. 8-33, we get

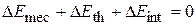
We can also let 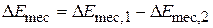, where the subscripts 1 and 2 refer to two different instants, say before and after a certain process has occurred. Then Eq. 8-34 becomes

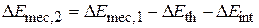
Equation 8-35 tells us:

In an isolated system, we can relate the total energy at one instant to the total energy at another instant without considering the energies at intermediate times.

This fact can be a very powerful tool in solving problems about isolated systems when you need to relate energies of a system before and after a certain process occurs in the system.

In Section 8-4, we discussed a special situation for isolated systems—namely, the situation in which nonconservative forces (such as a- kinetic frictional force) do not act within them. In that special situation, 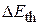and are both zero, and so Eq. 8-35 reduces to Eq. 8-18. In other words, the mechanical energy of an isolated system is conserved when nonconservative forces do not act within it.

Power

Now that you have seen how energy can be transferred from one form to another, we can expand the definition of power given in Section 7-7. There it is the rate at which work is done by a force. In a more general sense, power 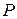is the rate at which energy is transferred by a force from one form to another. If an amount of energy 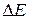is transferred in an amount of time , the average power due to the force is

Similarly, the instantaneous power due to the force is

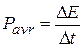(8-36)

Similarly, the instantaneous power due to the force is

(8-37)