Turning Points

In the absence of a nonconservative force, the mechanical energy 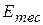of the system has a constant value given by

. (8-21)

Here 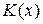is the kinetic energy function of the particle (this 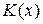gives the kinetic energy as a function of the particle's location x). We may rewrite Eq. 8-21 as

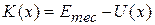(8-22)

Suppose that 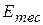(which has a constant value, remember) happens to be 5.0 J. It would be represented in Fig. 8-10a by a horizontal line that runs through the value 5.0 J on the energy axis. (It is, in fact, shown there.)

Equation 8-22 tells us how to determine the kinetic energy 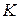for any location x of the particle: On the 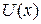curve, find U for that location x and then subtract U from 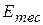For example, if the particle is at any point to the right of 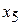, then К = 1.0 J. The value of К is greatest (5.0 J) when the particle is at x₂, and least (0 J) when the particle is at x_v

Since 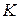can never be negative (because v² is always positive), the particle can never move to the left of 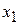_? where 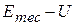is negative. Instead, as the particle moves toward 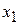from. x₂, К decreases (the particle slows) until К = 0 at 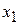(the particle stops there).

Note that when the particle reaches 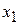, the force on the particle, given by Eq. 8-20, is positive (because the slope 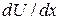is negative). This means that the particle does not remain at 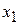but instead begins to move to the right, opposite its earlier motion. Hence 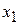is a turning point,a place where (because 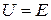) and the particle changes direction. There is no turning point (where ) on the right side of the graph. When the particle heads to the right, it will continue indefinitely.