Determining Potential Energy Values

Here we find equations that give the value of the two types of potential energy discussed in this chapter: gravitational potential energy and elastic potential energy. However, first we must find a general relation between a conservative force and the associated potential energy.

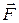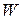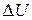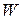Consider a particle-like object that is part of a system in which a conservative force acts. When that force does work on the object, the change in the potential energy associated with the system is the negative of the work done. We wrote this fact as Eq. 8-1 ( ). For the most general case, in which the force may vary with position, we may write the work as in Eq. 7-32:

(8-5)

This equation gives the work done by the force when the object moves from point 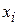, to point 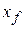, changing the configuration of the system. (Because the force is conservative, the work is the same for all paths between those two points.)

Substituting Eq. 8-5 into Eq. 8-1, we find that the change in potential energy due to the change in configuration is

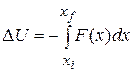(8-6)

This is the general relation we sought. Let's put it to use.