Path Independence of Conservative forces

The primary test for determining whether a force is conservative or nonconservative is this: Let the force act on a particle that moves along any closed path, beginning at some initial position and eventually returning to that position (so that the particle makes a round trip beginning and ending at the initial position). The force is con­servative only if the total energy it transfers to and from the particle during the round trip along this and any other closed path is zero. In other words:

The net work done by a conservative force on a particle moving around every closed path is zero.

We know from experiment that the gravitational force passes this closed-path test. An example is the tossed tomato of Fig. 8-2. The tomato leaves the launch point with speed 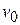and kinetic energy 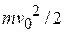. The gravitational force acting on the tomato slows it, stops it, and then causes it to fall back down. When the tomato returns to the launch point, it again has speed 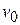and kinetic energy 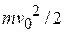. Thus, the gravitational force transfers as much energy from the tomato during the ascent as it transfers to the tomato during the descent back to the launch point. The net work done on the tomato by the gravitational force during the round trip is zero. An important result of the closed-path test is that

► The work done by a conservative force on a particle moving between two points does not depend on the path taken by the particle.

For example, suppose that a particle moves from point a to point b in Fig. 8-4a along either path 1 or path 2. If only a conservative force acts on the particle, then the work done on the particle is the same along the two paths. In symbols, we can write this result as

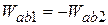(8-2)

where the subscript ab indicates the initial and final points, respectively, and the subscripts 1 and 2 indicate the path.

This result is powerful, because it allows us to simplify difficult problems when only a conservative force is involved. Suppose you need to calculate the work done by a conservative force along a given path between two points, and the calculation is difficult or even impossible without additional information. You can find the work by substituting some other path between those two points for which the calculation is easier and possible. Sample Problem 8-1 gives an example, but first we need to prove Eq. 8-2.