Work Done by a Gravitational force

We next examine the work done on an object by a particular type of force - namely, the gravitational force acting on it. Figure 7-6 shows a particle-like tomato of mass 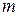that is thrown upward with initial speed 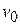and thus with initial kinetic energy 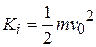. As the tomato rises, it is slowed by a gravitational force 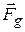; that is, the tomato's kinetic energy decreases because 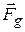does work on the tomato as it rises.

Because we can treat the tomato as a particle, we can use Eq. 7-7 ( 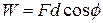) to express the work done during a displacement 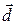. For the force magnitude , we use as the magnitude of 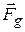. Thus, the work 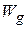done by the gravitational force 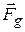,is

work done by gravitational force (7-12)

For a rising object, force 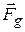is directed opposite the displacement 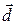, as indicated in Fig. 7-6. Thus, and

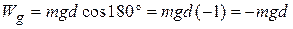(7-13)

The minus sign tells us that during the object's rise, the gravitational force on the object transfers energy in the amount from the kinetic energy of the object. This is consistent with the slowing of the object as it rises.

After the object has reached its maximum height and is falling back down, the angle 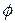between force 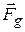and displacement 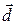is zero. Thus,

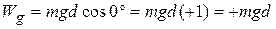
The plus sign tells us that the gravitational force now transfers energy in the amount to the kinetic energy of the object. This is consistent with the speeding up of the object as it falls. (Actually, as we shall see in Chapter 8, energy transfers associated with lifting and lowering an object involve not just the object, but the full object-Earth system. Without Earth, of course, "lifting" would be meaningless.)

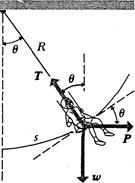
EXAMPLE 7—3 A child of weight sits on a swing of length , as shown in Fig. 7-7. A variable horizontal force , which starts at zero and gradually increases, is used to pull the child very slowly (so that equilibrium exists at all times) until the ropes make an angle with the vertical. Calculate the work of the force .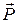

SOLUTION The body is in equilibrium, so the sum of the horizontal forces equals zero:

.

The sum of the vertical forces is also zero:

.

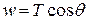Dividing these two equations, we find

.

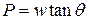The point of application of 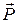swings through the arcs. Since 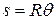, 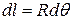and

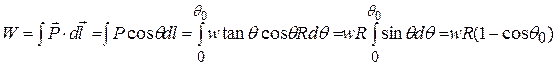
If 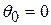, there is no displacement; in that case 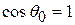and 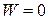, as expected. If 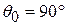°, then 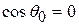and 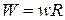. In that case the work is the same as though the body had been lifted straight up a distance 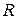by a force equal to its weight . In fact, as you should verify, the quantity 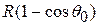is the increase in the height of the body during the displacement; so for any value of 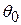, the work done by force 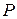is the change in height multiplied by the weight. We will prove this result more generally in Section 7—5.

EXAMPLE 7—10 In Jules Verne's story "From the Earth to the Moon" (written in 1865) three men were shot to the moon in a shell fired from a giant cannon sunk in the earth in Florida. What muzzle velocity would be needed (a) to raise a total mass m to a height above the earth equal to the earth's radius; (b) to escape from the earth completely? To simplify the calculation, neglect the gravitational pull of the moon.

SOLUTION

a) In Eq. (7-23), let 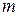be the total projectile mass and let 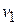be the initial velocity.

Then 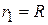, , 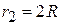and

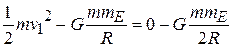or

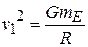
Then

b) When 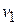is the escape velocity, 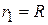, , 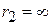. Then

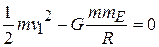or ,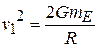

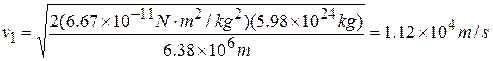
Note that the speed of an earth satellite in a circular orbit of radius just slightly greater than 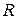is, from Eq. (6—22), the same as the result of part (a), and that the escape velocity is larger than this by exactly a factor of .