Work-Kinetic Energy Theorem

Equation 7-5 relates the change in kinetic energy of the bead (from an initial 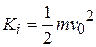to a later 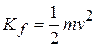) to the work 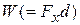done on the bead. For such particle-like objects, we can generalize that equation. Let 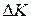be the change in the kinetic energy of the object, and 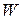the net work done on it. Then we can write

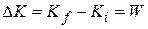(7-10)

which says that

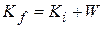(7-11)

which says that

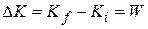
These statements are known traditionally as the work-kinetic energy theorem for particles. They hold for both positive and negative work: If the net work done on a particle is positive, then the particle's kinetic energy increases by the amount of the work. If the net work done is negative, then the particle's kinetic energy decreases by the amount of the work.

For example, if the kinetic energy is initially 5 J and there is a net transfer of 2 J to the particle (positive net work), then the final kinetic energy is 7 J. If, instead, there is a net transfer of 2 J from the particle (negative net work), then the final kinetic energy is 3 J.

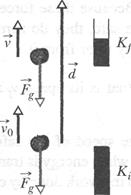
Fig. 7-6 A particle-like tomato of mass m thrown upward slows from velocity 7₀ to velocity ~v during displacement d because the gravitational force F_g acts on it. A kinetic energy gauge indicates the resulting change in the kinetic energy of the object, from ЛГ, (= {mv§) to K_f{= \mv²).