Rocket Propulsion (Example of Variable Mass Situation)

The principle of conservation of momentum can be applied to study the motion of a rocket. This application is of special significance as rocket is a system in which mass varies with time.

v+dv

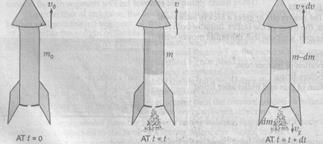
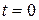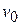Consider a rocket (may be a multistage rocket) moving vertically upwards from the surface of earth. Suppose that at time , the mass of the rocket (mass of container and fuel) is and is moving with velocity w.r.t. earth as shown in Fig. 1.05a. Let at any time , mass of the rocket be 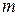and its velocity be 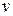(Fig. 1.05b/). The velocity of the rocket increases due to the combustion of the fuel. Thus, and . Suppose that in the time interval between and 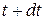, the mass 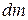of the fuel gets burnt and the velocity of the rocket increases to . 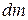The mass of the fuel leaves the rocket in downward direction in the form of burnt gases with velocity 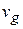w.r.t. earth (Fig. 1.05c).

According to the principle of conservation of momentum, the linear momentum of mass 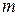of the rocket at time must be equal to the vector sum of the momentum of mass ( 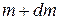)of the rocket and mass 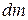in the form of burnt gases. Therefore,

. .(1.11)

The velocity of burnt gases has been taken as negative, as the burnt gases move in a direction opposite to that of the rocket. From equation (1.11), we have

The factor is product of two very small quantities and hence can be neglected. Therefore,

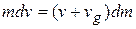...(1.12)

In the Eq.(1.12) 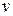represents the velocity of the rocket w.r.t. earth in upward direction 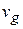represents the velocity of the burnt gases w.r.t. earth in downward direction. If is the relative velocity of the burnt gases w.r.t. the rocket, then

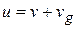(in downward direction)

Therefore, the Eq/(1.12) becomes

. ...(1.13)

The negative sign indicates that the velocity of the burnt gases w.r.t. the rocket i.e. is in downward direction.

Expression for velocity of rocket at any instant. From equation (1.13), we have

...(1.14)

Now, when , and when 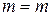, 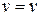.Therefore, integrating the equation within the proper limits, we have

.

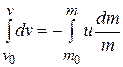Usually the exhaust velocity of the burnt gases is assumed to be constant throught the firing of the rocket. Therefore,

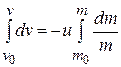
or

or

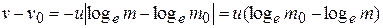
or

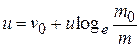...(1.15)

Therefore,

The Eq. (1.15) gives the velocity of the rocket at any time , when its mass is .

If at 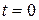the initial velocity of the rocket is zero, then the above equation becomes

...(1.15)

Thus, velocity of the rocket at any instant is directly proportional to

(i) the exhaust speed of the burnt gases and

(ii) the natural logarithm of the ratio of the initial mass of the rocket to its mass at that instant.

Thrust on the rocket. Dividing both sides of the equation (1.13) by 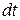, we have

Since represents the instantaneous acceleration of the rocket, is equal to the instantaneous force or thrust on the rocket. Therefore, thrust on the rocket,

(1.17)

Since the velocity of the burnt gases w.r.t. the rocket i.e. is in downward direction, it follows that the thrust on the rocket is in upward direction.

Here, denotes the instantaneous rate of consumption of the fuel in the rocket.

Thus, thrust on the rocket at any instant is equal to the product of the exhaust speed of the burnt gases and the rate of combustion of the fuel at that instant.

Burnt out speed of the rocket.The speed acquired by the rocket, when whole of the fuel gets burnt, is called the burnt out speed and it is the maximum speed that can be acquired by the rocket.

Therefore, when the rocket acquires the burnt-out speed ( 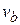) the mass of the rocket becomes equal to that of its empty container, say 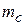i.e.

when ,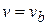

In the equation (1.15), setting the above condition, we have

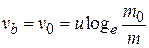...(1.18)

EXAMPLE 8—13 In the first second of its flight, a rocket ejects 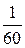of its mass with a relative velocity of 2400 m/s. What is the acceleration of the rocket?

SOLUTION We have 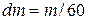, 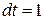s. From Eq. (8-34),

m/s².

EXAMPLE 8—14 Suppose the ratio of initial mass to final mass 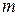for the rocket in Example 8—13 is 4, and that the fuel is consumed in a time t = 60 s. Find the rocket's velocity at the end of this time.

SOLUTION From Eq. (8-35),

.

At the start of the flight, when the velocity of the rocket is zero, the ejected gases are moving downward, relative to the earth, with a velocity equal to the relative velocity 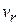. When the velocity of the rocket has increased to 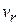, the ejected gases have a velocity zero relative to the earth. When the rocket velocity becomes greater than 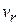, the velocity of the ejected gases is in the same direction as that of the rocket. Thus the velocity acquired by the rocket can be greater (and is often much greater) than the relative velocity 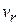. In the example above, where the final velocity of the rocket was 2740 m/s and the relative velocity was 2400 m/s, the last portion of the ejected fuel had an upward velocity (relative to the earth) of (2740 - 2400) m/s = 340 m/s.

Example 1.23. Fuel is consumed at the rate of 100 kg/s in a rocket. The exhaust gases are ejected at a speed of 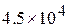m/s. What is the thrust experienced by the rocket? Also calculate velocity of the rocket at the instant, when its mass is reduced to l/10th of its initial mass.

Sol. Here, rate of consumption of the fuel,

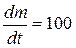kgm/s

speed with which the exhaust gases are ejected,

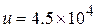m/s.

Now, thrust experienced by the rocket,

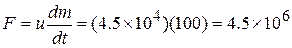N.

Also, Here, or .

m/s.