Newton's Second Law for a System of Particles

If you roll a cue ball at a second billiard ball that is at rest, you expect that the two-ball system will continue to have some forward motion after impact. You would be surprised, for example, if both balls came back toward you or if both moved to the right or to the left.

What continues to move forward, its steady motion completely unaffected by the collision, is the center of mass of the two-ball system. If you focus on this point— which is always halfway between these bodies because they have identical masses— you can easily convince yourself by trial at a billiard table that this is so. No matter whether the collision is glancing, head on, or somewhere in between, the center of mass continues to move forward, as if the collision had never occurred. Let us look into this center-of-mass motion in more detail.

To do so, we replace the pair of billiard balls with an assemblage of n particles of (possibly) different masses. We are interested not in the individual motions of these particles but only in the motion of their center of mass. Although the center of mass is just a point, it moves like a particle whose mass is equal to the total mass of the system; we can assign a position, a velocity, and an acceleration to it. We state (and shall prove next) that the (vector) equation that governs the motion of the center of mass of such a system of particles is

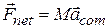(system of particles). (9-14)

This equation is Newton's second law for the motion of the center of mass of a system of particles. Note that it has the same form (F_net = ma) that holds for the motion of a single particle. However, the three quantities that appear in Eq. 9-14

must be evaluated with some care:

1. 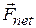is the net force of all external forces that act on the system. Forces on one part of the system from another {internal forces) are not included in Eq. 9-14,

2. 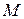is the total mass of the system. We assume that no mass enters or leaves the system as it moves, so that 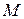remains constant. The system is said to be closed.

3. 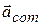is the acceleration of the center of mass of the system. Equation 9-14 gives no information about the acceleration of any other point of the system.

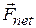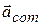Equation 9-14 is equivalent to three equations involving the components of and along the three coordinate axes. These equations are

, ,

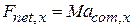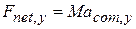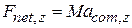
Now we can go back and examine the behavior of the billiard balls. Once the cue ball has begun to roll, no net external force acts on the (two-ball) system. Thus, because 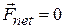, Eq. 9-14 tells us that 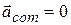also. Because acceleration is the rate of change of velocity, we conclude that the velocity of the center of mass of the system of two balls does not change. When the two balls collide, the forces that come into play are internal forces, on one ball from the other. Such forces do not contribute to the net force 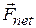, which remains zero. Thus, the center of mass of the system, which was moving forward before the collision, must continue to move forward after the collision, with the same speed and in the same direction.

Equation 9-14 applies not only to a system of particles but also to a solid body, such as the bat of Fig. 9-lb. In that case, 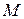in Eq. 9-14 is the mass of the bat and F_net is the gravitational force on the bat. Equation 9-14 then tells us that 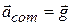. In other words, the center of mass of the bat moves as if the bat were a single particle of mass 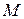, with force 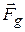acting on it.

Figure 9-5 shows another interesting case. Suppose that at a fireworks display, a rocket is launched on a parabolic path. At a certain point, it explodes into fragments. If the explosion had not occurred, the rocket would have continued along the tra­jectory shown in the figure. The forces of the explosion are internal to the system (first the rocket and then its fragments); that is, they are forces on parts of the system from other parts. If we ignore air drag, the net external force 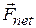acting on the system is the gravitational force on the system, regardless of whether the rocket explodes. Thus, from Eq. 9-14, the acceleration 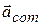of the center of mass of the fragments (while they are in flight) remains equal to 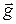. This means that the center of mass of the fragments follows the same parabolic trajectory that the rocket would have followed had it not exploded.

When a ballet dancer leaps across the stage in a grand jete, she raises her arms and stretches her legs out horizontally as soon as her feet leave the stage (Fig. 9-6). These actions shift her center of mass upward through her body. Although the shift­ing center of mass faithfully follows a parabolic path across the stage, its movement relative to the body decreases the height that is attained by her head and torso, relative to that of a normal jump. The result is that the head and torso follow a nearly horizontal path, giving an illusion that the dancer is floating.