Sample Problem 9-2
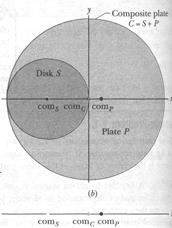
Figure 9-4a shows a uniform metal plate P of radius 2R from which a disk of radius R has been stamped out (removed) in an assembly line. Using the xy coordinate system shown, locate the center of mass comP of the plate.
SOLUTION: First, let us roughly locate the center of plate P by using the Key Idea of symmetry. We note that the plate is symmetric about the  axis (we get the portion below that axis by rotating the upper portion about the axis). Thus, comP must be on the
axis (we get the portion below that axis by rotating the upper portion about the axis). Thus, comP must be on the  axis. The plate (with the disk removed) is not symmetric about the
axis. The plate (with the disk removed) is not symmetric about the  axis. However, because there is somewhat more mass on the right of the
axis. However, because there is somewhat more mass on the right of the  axis, comP must be somewhat to the right of that axis. Thus, the location of comP should be roughly as indicated in Fig. 9-4a.
axis, comP must be somewhat to the right of that axis. Thus, the location of comP should be roughly as indicated in Fig. 9-4a.
Another Key Idea here is that plate P is an extended solid body, so we can use Eqs. 9-11 to find the actual coordinates of comP. However, that procedure is difficult. A much easier way is to use this Key Idea: In working with centers of mass, we can assume that the mass of a uniform object is concentrated in a particle at the object's center of mass. Here is how we do so:
First, put the stamped-out disk (call it disk S) back into place (Fig. 9-4b) to form the original composite plate (call it plate C). Because of its circular symmetry, the center of mass comS for disk S is at the center of S, at 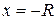 (as shown). Similarly, the center of mass comc for composite plate С is at the center of C, at the origin (as shown). We then have the following:
(as shown). Similarly, the center of mass comc for composite plate С is at the center of C, at the origin (as shown). We then have the following:
| Center | Location | |||
| Plate | of Mass | of com | Mass | |
| P | comf | xP = ? | mP | |
| S | coms | xs= -R | ms | |
| С | comc | xc = 0 | mc | ms + mP |

|
Now we use the Key Idea of concentrated mass: Assume that mass ms of disk S is concentrated in a particle at 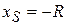 , and mass mPis concentrated in a particle at xP (Fig. 9-4c). Next treat these two particles as a two-particle system, using Eq. 9-2 to find their center of mass xs+P. We get
, and mass mPis concentrated in a particle at xP (Fig. 9-4c). Next treat these two particles as a two-particle system, using Eq. 9-2 to find their center of mass xs+P. We get
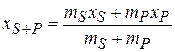 (9-12)
(9-12)
Next note that the combination of disk S and plate P is composite plate С Thus, the position xs+P of comS+P must coincide with the position xc of comc, which is at the origin; so xs+P = xc = 0. Substituting this into Eq. 9-12 and solving for xP, we get
|
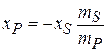 (9-13)
(9-13)
Now we seem to have a problem, because we do not know the masses in Eq. 9-13. However, we can relate the masses to the face areas of S and P by noting that
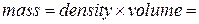
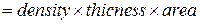
Then
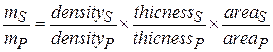
Because the plate is uniform, the densities and thicknesses are equal; we are left with
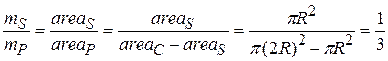
Substituting this and 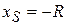 into Eq. 9-13, we have
into Eq. 9-13, we have
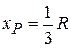
PROBLEM-SOLVING TACTICS
Center-of-Mass Problems
Sample Problems 9-1 and 9-2 provide three strategies for simplifying center-of-mass problems. (1) Make full use of the symmetry of the object, be it about a point, a line, or a plane. (2) If the object can be divided into several parts, treat each of these parts as a particle, located at its own center of mass. (3) Choose your axes
wisely: If your system is a group of particles, choose one of the particles as your origin. If your system is a body with a line of symmetry, let that be your x or у axis. The choice of origin is completely arbitrary; the location of the center of mass is the same regardless of the origin from which it is measured.
Дата добавления: 2015-06-17; просмотров: 875;
