Systems of Particles

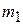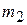Figure 9-2a shows two particles of masses and separated by a distance 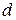. We have arbitrarily chosen the origin of the x axis to coincide with the particle of mass 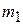. We define the position of the center of mass (com) of this two-particle system to be

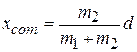(9-1)

Suppose, as an example, that 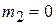. Then there is only one particle, of mass 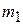, and the center of mass must lie at the position of that particle; Eq. 9-1 dutifully reduces to 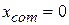. If 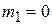, there is again only one particle (of mass 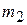), and we have, as we expect, 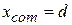. If 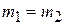, the masses of the particles are equal and the center of mass should be halfway between them; Eq. 9-1 reduces to ,again as we expect. Finally, Eq. 9-1 tells us that if neithe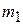r nor 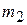is zero, 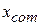can have only values that lie between zero and 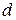; that is, the center of mass must lie somewhere between the two particles.

Fig. 9-2 (a) Two particles of masses 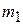and 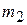are separated by a distance 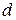. The dot labeled com shows the position of the center of mass, calculated from Eq. 9-1. (b) The same as (a) except that the origin is located farther from the particles. The position of the center of mass is calculated from Eq. 9-2. The location of the center of mass (with respect to the particles) is the same in both cases.

Figure 9-2b shows a more generalized situation, in which the coordinate system has been shifted leftward. The position of the center of mass is now defined as

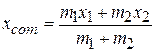(9-2)

Note that if we put 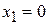, then 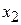becomes 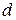and Eq. 9-2 reduces to Eq. 9-1, as it must. Note also that in spite of the shift of the coordinate system, the center of mass is still the same distance from each particle. We can rewrite Eq. 9-2 as

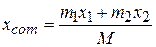(9-3)

in which M is the total mass of the system. (Here, .) We can extend this equation to a more general situation in which 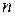particles are strung out along the x axis. Then the total mass is , and the location of the center of mass is

(9-4)

Here the subscript 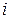is a running number, or index, that takes on all integer values from 1 to n. It identifies the various particles, their masses, and their x coordinates. If the particles are distributed in three dimensions, the center of mass must be identified by three coordinates. By extension of Eq. 9-4, they are

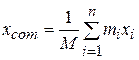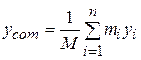
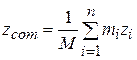, (9-j)

We can also define the center of mass with the language of vectors. First recall that the position of a particle at coordinates 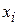, 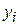and 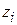, is given by a position vector:

. (9-6)

Here the index identifies the particle, an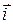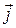d , , and 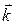are unit vectors pointing, respectively, in the positive direction of the x, y, and z axes. Similarly, the position of the center of mass of a system of particles is given by a position vector:

. (9-7)

The three scalar equations of Eq. 9-5 can now be replaced by a single vector equation,

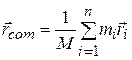. (9-8)

where again M is the total mass of the system. You can check that this equation is correct by substituting Eqs. 9-6 and 9-7 into it, and then separating out the x, y, and z components. The scalar relations of Eq. 9-5 result.