Solid Bodies

An ordinary object, such as a baseball bat, contains so many particles (atoms) that we can best treat it as a continuous distribution of matter. The "particles" then become differential mass elements dm, the sums of Eq. 9-5 become integrals, and the coordinates of the center of mass are defined as

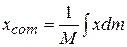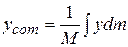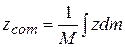, , (9-9)

where 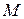is now the mass of the object.

Evaluating these integrals for most common objects (like a television set or a moose) would be difficult, so here we shall consider only uniform objects. Such an object has uniform density, or mass per unit volume; that is, the density p (Greek letter rho) is the same for any given element of the object as for the whole object: 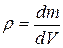(9-10)

where dV is the volume occupied by a mass element 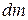, and V is the total volume of the object. If we substitute 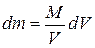from Eq. 9-10 into Eq. 9-9, we find that

, ,

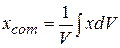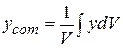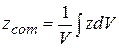
You can bypass one or more of these integrals if an object has a point, a line, or a plane of symmetry. The center of mass of such an object then lies at that point, on that line, or in that plane. For example, the center of mass of a uniform sphere (which has a point of symmetry) is at the center of the sphere (which is the point of symmetry). The center of mass of a uniform cone (whose axis is a line of symmetry) lies on the axis of the cone. The center of mass of a banana (which has a plane of symmetry that splits it into two equal parts) lies somewhere in that plane.

The center of mass of an object need not lie within the object. There is no dough at the center of mass of a doughnut, and no iron at the center of mass of a horseshoe.

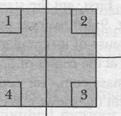
Checkpoint i: The figure shows a uniform square

plate from which four identical squares at the corners will be removed, (a) Where is the center of mass of the plate originally? Where is it after the removal of (b) square 1; (c) squares 1 and 2; (d) squares 1 and 3; (e) squares 1, 2, and 3; (f) all four squares? Answer in terms of quadrants, axes, or points (without calculation, of course).