Sample Problem 9-3

The three particles in Fig. 9-1 a are initially at rest. Each experiences an external force due to bodies outside the three-particle system. The directions are indicated, and the magnitudes are 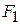= 6.0 N, 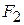= 12 N, and 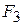= 14 N. What is the acceleration of the center of mass of the system, and in what direction does it move?

SOLUTION: The position of the center of mass, calculated by the method of Sample Problem 9-1, is marked by a dot in the figure. One Key Idea here is that we can treat the center of mass as if it were a real particle, with a mass equal to the system's total mass M = 16 kg. We can also treat the three external forces as if they act at the center of mass (Fig. 9-lb).

A second Key Idea is that we can now apply Newton's second law ( 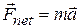) to the center of mass, writing

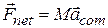
or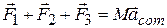

so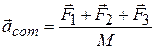

Equation 9-20 tells us that the acceleration 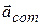of the center of mass is in the same direction as the net external force 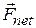on the system (Fig. 9-lb). Because the particles are initially at rest, the center of mass must also be at rest. As the center of mass then begins to accelerate, it must move off in the common direction of 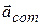and .

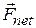We can evaluate the right side of Eq. 9-21 directly on a vector-capable calculator, or we can rewrite Eq. 9-21 in component form, find the components of 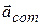, and then find 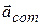. Along the x axis, we have

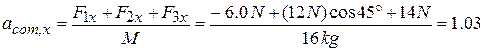m/s².

Along the у axis, we have

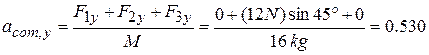m/s².

From these components, we find that 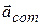has the magnitude

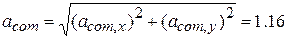m/s².

and the angle (from the positive direction of the x