Work-Kinetic Energy Theorem with a Variable Force

Equation 7-32 gives the work done by a variable force on a particle in a one-dimensional situation. Let us now make certain that the work calculated with Eq. 7-32 is indeed equal to the change in kinetic energy of the particle, as the work-kinetic energy theorem states.

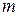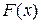Consider a particle of mass , moving along the axis and acted on by a net force that is directed along that axis. The work done on the particle by this force as the particle moves from an initial position 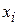to a final position 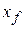is given by Eq. 7-32 as

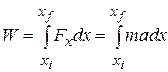(7-37)

in which we use Newton's second law to replace 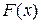with 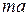. We can write the quantity

(7-38)

in Eq. 7-37 as

From the "chain rule" of calculus, we have

(7-39)

and Eq. 7-38 becomes

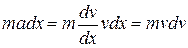(7-40)

Substituting (7-40) into 7-37 yields

(7-41)

Note that when we change the variable from to 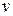we are required to express the limits on the integral in terms of the new variable. Note also that because the mass m is a constant, we are able to move it outside the integral.

Recognizing the terms on the right side of Eq. 7-41 as kinetic energies allows us to write this equation as

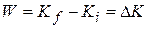
which is the work-kinetic energy theorem.