Three-Dimensional Analysis

Consider now a particle that is acted on by a three-dimensional force

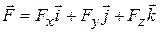(7-33

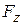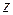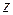in which the components , , and can depend on the position of the particle that is, they can be functions of that position. However, we make three simplifications: may depend on but not on or , may depend on but not on or , and 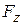may depend on 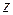but not on or . Now let the particle move through an incremental displacement

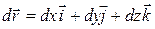(7-34)

The increment of work 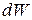done on the particle by 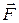during the displacement 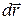is, by Eq. 7-8,

(7-35)

The work 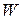done by 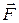while the particle moves from an initial position 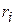with coordinates ( 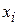, , 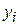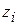) to a final position with coordinates ( 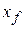, , 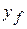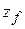) is then

(7-36)

If 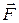has only an component, then the and 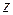terms in Eq. 7-36 are zero and the equation reduces to Eq. 7-32.