Proof of the Parallel-Axis Theorem

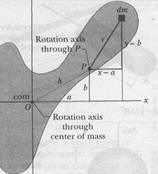Fig. 11-12

Let О be the center of mass of the arbitrarily shaped body shown in cross section in Fig. 11-12. Place the origin of the coordinates at O. Consider an axis through O perpendicular to the plane of the figure, and another axis through point P parallel to the first axis. Let the x and у coordinates of P be a and b.

Let 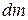be a mass element with the general coordinates x and y. The rotational inertia of the body about the axis through P is then, from Eq. 11-28,

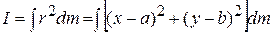
which we can rearrange as

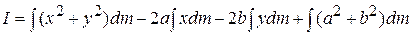11-30

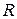From the definition of the center of mass (Eq. 9-9), the middle two integrals of Eq. 11-30 give the coordinates of the center of mass (multiplied by a constant) and thus must each be zero. Because is equal to , where is the distance from О to 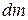, the first integral is simply 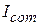, the rotational inertia of the body about an axis through its center of mass. Inspection of Fig. 11-12 shows that the last term in Eq. 11-30 is 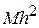, where 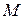is the body's total mass. Thus, Eq. 11-30 reduces to Eq. 11-29, which is the relation that we set out to prove.