Proof of Eqs. 11-44 through 11-47

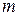Let us again consider the situation of Fig. 11-16, in which force rotates a rigid body consisting of a single particle of mass fastened to the end of a massless rod. During the rotation, force does work on the body. Let us assume that the only energy of the body that is changed by is the kinetic energy. Then we can apply the work-kinetic energy theorem of Eq. 11-41

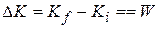. 11-48

Using 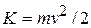and Eq 11-18 ( 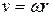) we can rewrite Eq. 11-48 as

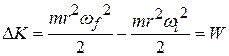
(11-

From Eq. 11-26, the rotational inertia for this one-particle body is 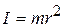. Substituting this into Eq. 11-49 yields

,

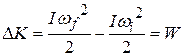which is Eq. 11-44. We derived it for a rigid body with one particle, but it holds for any rigid body rotated about a fixed axis.

We next relate the work 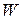done on the body in Fig. 11-16 to the torque 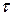оп the body due to force . When the particle moves a distance 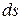along its circular path, only the tangential component F_t of the force accelerates the particle along the path. Therefore, only does work on the particle. We write that work . However, we can replace 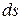with 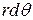, where is the angle through which the particle moves. Thus we have

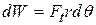. (11-50)

From Eq. 11-32, we see that the product 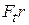is equal to the torque 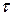, so we can rewrite Eq. 11-50 as

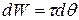(11-51)

The work done during a finite angular displacement from 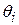to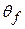

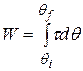
which is Eq. 11-45. It holds for any rigid body rotating about a fixed axis. Equation 11-46 comes directly from Eq. 11-45.

We can find the power P for rotational motion from Eq. 11-51:

which is Eq. 11-47