Newton's Second Law for Rotation
A torque can cause rotation of a rigid body, as when you use a torque to rotate a door. Here we want to relate the net torque 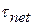 on a rigid body to the angular acceleration
on a rigid body to the angular acceleration 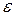 it causes about a rotation axis. We do so by analogy with Newton's second law (
it causes about a rotation axis. We do so by analogy with Newton's second law ( 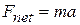 ) for the acceleration a of a body of mass
) for the acceleration a of a body of mass 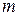 due to a net force
due to a net force 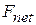 along a coordinate axis. We replace
along a coordinate axis. We replace 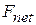 with
with 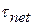 ,
, 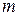 with
with 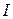 , and
, and 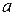 with
with 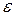 , writing
, writing
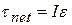 (Newton's second law for rotation), 11-34
(Newton's second law for rotation), 11-34
where 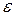 must be in radian measure.
must be in radian measure.
Proof of Equation 11-34
We prove Eq. 11-34 by first considering the simple situation shown in Fig. 11-16.

|
The rigid body there consists of a particle of mass 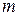 on one end of a massless rod of length
on one end of a massless rod of length 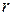 . The rod can move only by rotating about its other end, around a rotation axis (an axle) that is perpendicular to the plane of the page. Thus, the particle can move only in a circular path that has the rotation axis at its center.
. The rod can move only by rotating about its other end, around a rotation axis (an axle) that is perpendicular to the plane of the page. Thus, the particle can move only in a circular path that has the rotation axis at its center.
A force  acts on the particle. However, because the particle can move only along the circular path, only the tangential component
acts on the particle. However, because the particle can move only along the circular path, only the tangential component 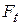 of the force (the component that is tangent to the circular path) can accelerate the particle along the path. We can relate
of the force (the component that is tangent to the circular path) can accelerate the particle along the path. We can relate 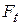 to the particle's tangential acceleration
to the particle's tangential acceleration 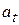 along the path with Newton's second law, writing
along the path with Newton's second law, writing
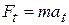 .
.
The torque acting on the particle is, from Eq. 11-32,
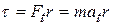 .
.
From Eq. 11-22 (  ) we can write this as
) we can write this as
 11-35
11-35
The quantity in parentheses on the right side of Eq. 11-35 is the rotational inertia of the particle about the rotation axis (see Eq. 11-26). Thus, Eq. 11-35 reduces to
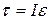
For the situation in which more than one force is applied to the particle, we can generalize Eq. 11-26 as
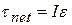
which we set out to prove. We can extend this equation to any rigid body rotating about a fixed axis, because any such body can always be analyzed as an assembly of single particles.
11-10 Work and Rotational Kinetic Energy
As we discussed in Chapter 7, when a force 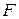 causes a rigid body of mass
causes a rigid body of mass 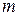 to accelerate along a coordinate axis, it does work
to accelerate along a coordinate axis, it does work 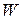 on the body. Thus, the body's kinetic energy (
on the body. Thus, the body's kinetic energy ( 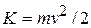 ) can change. Suppose it is the only energy of the body that changes. Then we relate the change
) can change. Suppose it is the only energy of the body that changes. Then we relate the change 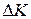 in kinetic energy to the work
in kinetic energy to the work 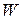 with the work-kinetic energy theorem (Eq. 7-10), writing
with the work-kinetic energy theorem (Eq. 7-10), writing
 (work-kinetic energy theorem). (11-41)
(work-kinetic energy theorem). (11-41)
For motion confined to an  axis, we can calculate the work with Eq. 7-32,
axis, we can calculate the work with Eq. 7-32,

This reduces to 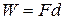 when
when 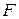 is constant and the body's displacement is d.
is constant and the body's displacement is d.
The rate at which the work is done is the power, which we can find with Eqs. 7-43
 (power, one-dimensional motion). (11-43)
(power, one-dimensional motion). (11-43)
Now let us consider a rotational situation that is similar. When a torque accelerates a rigid body in rotation about a fixed axis, it does work 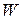 on the body. Therefore, the body's rotational kinetic energy (
on the body. Therefore, the body's rotational kinetic energy ( 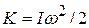 ) can change. Suppose that it is the only energy of the body that changes. Then we can still relate the change
) can change. Suppose that it is the only energy of the body that changes. Then we can still relate the change 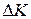 in kinetic energy to the work
in kinetic energy to the work 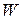 with the work-kinetic energy theorem, except now the kinetic energy is a rotational kinetic energy:
with the work-kinetic energy theorem, except now the kinetic energy is a rotational kinetic energy:
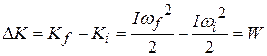 (work-kinetic energy theorem). (11-44)
(work-kinetic energy theorem). (11-44)
Here, 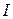 is the rotational inertia of the body about the fixed axis and
is the rotational inertia of the body about the fixed axis and 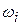 and
and 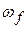 are the angular speeds of the body before and after the work is done, respectively. Also, we can calculate the work with a rotational equivalent of Eq. 11-42,
are the angular speeds of the body before and after the work is done, respectively. Also, we can calculate the work with a rotational equivalent of Eq. 11-42,
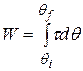 (work, rotation about fixed axis),(11-45)
(work, rotation about fixed axis),(11-45)
where 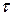 is the torque doing the work
is the torque doing the work 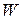 , and
, and 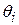 and
and 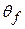 are the body's angular positions before and after the work is done, respectively. When
are the body's angular positions before and after the work is done, respectively. When 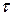 is constant, Eq. 11-45 reduces to
is constant, Eq. 11-45 reduces to
 (work, constant torque). (11-46)
(work, constant torque). (11-46)
The rate at which the work is done is the power, which we can find with the rotational equivalent of Eq. 11-43,
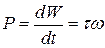 power, rotation about fixed axis). (11-47)
power, rotation about fixed axis). (11-47)
Дата добавления: 2015-06-17; просмотров: 776;
