ТО FIND MOMENT OF INERTIA OF A RIGID BODY
The moment of inertia of a symmetrical body rotating about its axis of symmetry can be found by finding the moment of inertia of a small element of it about the axis of rotation and then integrating it within the proper limits for whole of the body.
Consider that a small elementary portion of mass 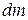 of the rigid body rotates about the axis of rotation at a distance
of the rigid body rotates about the axis of rotation at a distance 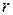 from it. Then, moment of inertia of the small elementary portion about the axis of rotation,
from it. Then, moment of inertia of the small elementary portion about the axis of rotation,
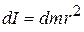
The moment of inertia of the whole rigid body about the axis of rotation,
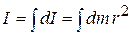 ...(3.09)
...(3.09)
If the rigid body is made of material of uniform density 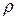 and
and 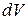 is the volume of the elementary portion of the body, then
is the volume of the elementary portion of the body, then 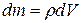 .Hence, moment of inertia of the rigid body about the axis of rotation,
.Hence, moment of inertia of the rigid body about the axis of rotation,
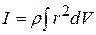 ...(3.10)
...(3.10)
In using this equation, we express the volume element dV in terms of the differentials of the integration variables, usually the coordinates of the volume elements. The element dV mustalways be chosen so that all points within it are at very nearly the same distance from the axis of rotation. For regularly shaped bodies this integration can be after be carried out quite easily. Discuss several examples.
In case the rigid body is a plane lamina,
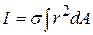
where dA is area of the elementary portion of the plane lamine and 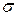 its mass per unit area.
its mass per unit area.
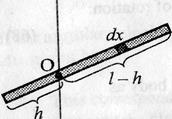
5.3.1. Uniform slender rod; axis perpendicular to length rod
Rod has mass 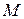 and length
and length 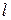 . We wish to compute its moment of inertia about an axis through O, at an arbitrary distance from one end. Using Eq. (70), we choose as an element of mass a short section having length
. We wish to compute its moment of inertia about an axis through O, at an arbitrary distance from one end. Using Eq. (70), we choose as an element of mass a short section having length 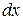 at a distance
at a distance 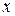 from point O.
from point O.
|
The ratio of the mass 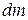 of this element to the total mass
of this element to the total mass 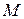 is equal to the ratio of its length
is equal to the ratio of its length 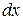 to the total length
to the total length 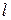 .Thus
.Thus 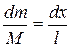
Where 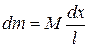
Using (70) we obtain:
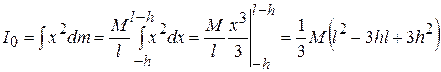 .
.
From this general expression we can find the moment of inertia about an axis through any point of the rod. For example, if the axis is at the left end, 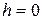 and
and
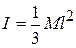
If the axis is the right end 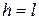 and
and 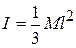
As would be expected, if the axis passes though the center,
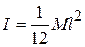
Дата добавления: 2015-06-17; просмотров: 782;
