Решение задач на определение скорости.
Для определения искомых кинематических характеристик (угловой скорости тела или скоростей его точек) надо знать модуль и направление скорости какой-нибудь одной точки и направление скорости другой точки сечения этого тела. С определения этих характеристик по данным задачи и следует начинать решение.
Механизм, движение которого исследуется, надо изображать на чертеже в том положении, для которого требуется определить соответствующие характеристики. При расчете следует помнить, что понятие о мгновенном центре скоростей имеет место для данного твердого тела. В механизме, состоящем из нескольких тел, каждое непоступательное движущееся тело имеет в данный момент времени свой мгновенный центр скоростей Р и свою угловую скорость.
Пример 8. Тело, имеющее форму катушки, катится своим средним цилиндром по неподвижной плоскости так, что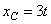 
(см). Радиусы цилиндров: R = 4 см и r = 2 см (рис.36). .
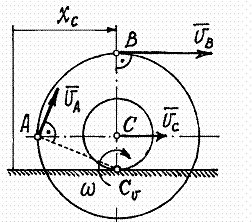
Рис.36
Определим скорости точек А,В и С.
Мгновенный центр скоростей находится в точке касания катушки с плоскостью.
Скорость полюса С .
.
|
Угловая скорость катушки
.
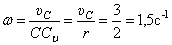Скорости точек А и В направлены перпендикулярно отрезкам прямых, соединяющих эти точки с мгновенным центром скоростей. Величина скоростей:
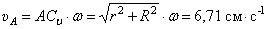
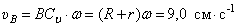
Пример 9. Стержень АВ скользит концами по взаимно перпендикулярным прямым так, что при угле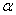 
скорость 
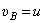. Длина стержня 
. Определим скорость конца А и угловую скорость стержня.
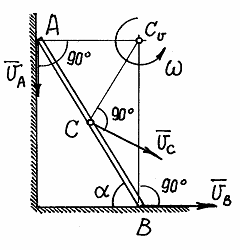
Рис.37
Нетрудно определить направление вектора скорости точки А, скользящей по вертикальной прямой. Тогда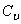 
находится на пересечении перпендикуляров к 
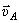и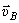 
(рис. 37).
Угловая скорость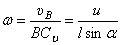 
.
Скорость точки А: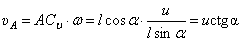 
.
|
А скорость центра стержня С, например, направлена перпендикулярно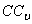 
и равна:
.
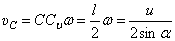План скоростей.
Пусть известны скорости нескольких точек плоского сечения тела (рис.38). Если эти скорости отложить в масштабе из некоторой точки О и соединить их концы прямыми, то получится картинка, которая называется планом скоростей. (На рисунке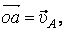 
).
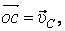
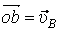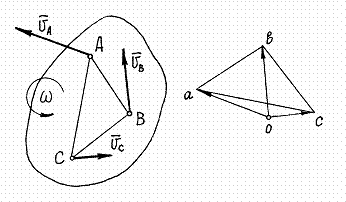
Рис.38
Свойства плана скоростей.
|
а) Стороны треугольников на плане скоростей перпендикулярны соответствующим прямым на плоскости тела.
Действительно,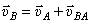 
. Но на плане скоростей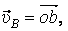 
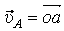. Значит 
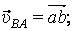причём 
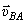перпендикулярна АВ, поэтому и 
. Точно так же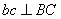 
и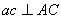 
.
б) Стороны плана скоростей пропорциональны соответствующим отрезкам прямых на плоскости тела.
Так как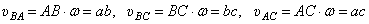 
, то отсюда и следует, что стороны плана скоростей пропорциональны отрезкам прямых на плоскости тела.
Объединив оба свойства, можно сделать вывод, что план скоростей подобен соответствующей фигуре на теле и повёрнут относительно её на 90˚ по направлению вращения. Эти свойства плана скоростей позволяют определять скорости точек тела графическим способом.
Пример 10. На рисунке 39 в масштабе изображён механизм. Известна угловая скорость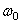 
звена ОА.
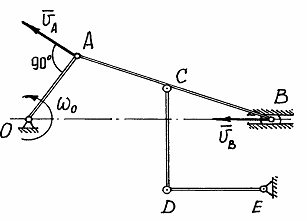
Рис.39
Чтобы построить план скоростей должна быть известна скорость какой-нибудь одной точки и хотя бы направление вектора скорости другой. В нашем примере можно определить скорость точки А: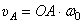 
и направление её вектора .
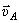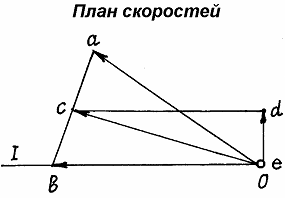
Рис.40
|
|
Откладываем (рис. 40) из точки о в масштабе 
Известно направление вектора скорости ползуна В – горизонтальное. Проводим на плане скоростей из точки О прямую I по направлению скорости 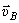, на которой должна находиться точка b, определяющая скорость этой точкиВ. Так как стороны плана скоростей перпендикулярны соответствующим звеньям механизма, то из точки а проводим прямую перпендикулярно АВ до пересечения с прямой I. Точка пересечения определит точку b, а значит и скорость точки В: 
. По второму свойству плана скоростей его стороны подобны звеньям механизма. Точка С делит АВ пополам, значит и с должна делить аb пополам. Точка с определит на плане скоростей величину и направление скорости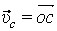 
(если с соединить с точкой О).
Скорость точки Е равна нулю, поэтому точка е на плане скоростей совпадает с точкой О.
Далее. Должно быть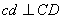 
и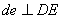 
. Проводим эти прямые, находим их точку пересечения d. Отрезок оd определит вектор скорости 
.
Дата добавления: 2015-06-17; просмотров: 1512;