Определение скоростей точек плоской фигуры

Было отмечено, что движение плоской фигуры можно рассматривать как слагающееся из поступательного движения, при котором все точки фигуры движутся со скоростью 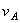полюса А, и из вращательного движения вокруг этого полюса. Покажем, что скорость любой точки М фигуры складывается геометрически из скоростей, которые точка получает в каждом из этих движений.

В самом деле, положение любой точки М фигуры определяется по отношению к осям Оху радиусом-вектором 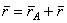(рис.30), где 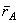- радиус-вектор полюса А, 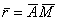- вектор, определяю­щий положение точки М относительно осей 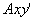, перемещающих­ся вместе с полюсом Апоступательно (движение фигуры по отноше­нию к этим осям представляет собой вращение вокруг полюса А). Тогда

.

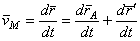В полученном равенстве величина 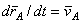есть скорость полюса А; величина же 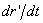равна скорости 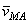, которую точка М получает при 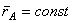, т.е. относительно осей 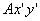, или, иначе говоря, при вращении фигуры вокруг полюса А. Таким образом, из предыдущего равенства действительно следует, что

.

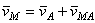Скорость 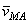, которую точка М получает при вращении фигуры вокруг полюса А:

,

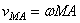
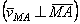где 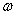- угловая скорость фигуры.

Таким образом, скорость любой точки М плоской фигуры геометрически складывается из скорости какой-нибудь другой точки А, принятой за полюс, и скорости, которую точка М получает при вращении фигуры вокруг этого полюса. Модуль и направление скорости 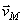находятся построением соответствующего параллело­грамма (рис.31).

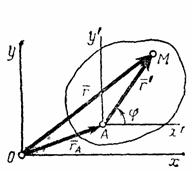
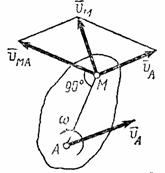
Рис.30 Рис.31

Теорема о проекциях скоростей двух точек тела

Определение скоростей точек плоской фигуры (или тела, дви­жущегося плоскопараллельно) связано обычно с довольно сложными расчетами. Однако можно получить ряд других, практически более удобных и простых мето­дов определения скоростей точек фигуры (или тела).

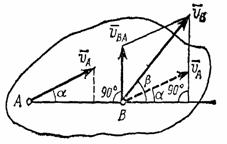
Рис.32

Один из таких методов дает тео­рема: проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу. Рассмотрим какие-нибудь две точки А и В плоской фигуры (или тела). Принимая точку А за полюс (рис.32), получаем 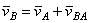. Отсюда, проектируя обе части равенства на ось, направленную по АВ, и учитывая, что вектор 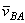перпендику­лярен АВ, находим

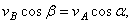
и теорема доказана.