Вращение тела вокруг неподвижной точки
Название такого вида движения довольно точно его определяет. Часто это движение называют сферическим движением потому, что все точки тела движутся по сферическим поверхностям.
Наглядным примером такого движения является волчок, закономерности движения которого лежат в основе гироскопических приборов.
1) Углы Эйлера. Уравнения вращения тела с одной неподвижной точкой.
|
|
Положение тела определяется тремя углами. Используются различные системы углов. Например, корабельные углы, самолётные углы и др. Но самыми распространёнными являются углы Эйлера: 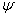 (пси),
(пси), 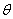 (тета),
(тета),  (фи).
(фи).
Положение тела определяется следующим образом. Назначаются две системы декартовых осей. Первая система – неподвижные оси 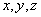 . Начало которых берётся в неподвижной точке
. Начало которых берётся в неподвижной точке 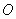 тела (рис. 20). Вторая система, оси
тела (рис. 20). Вторая система, оси 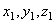 , связывается с телом. Поэтому положение тела будет определяться как положение этих осей относительно неподвижных.
, связывается с телом. Поэтому положение тела будет определяться как положение этих осей относительно неподвижных.
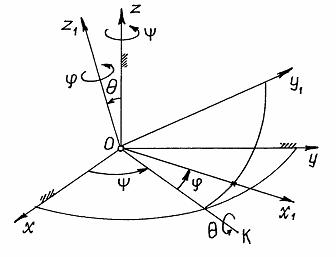
Рис.20
|
|
Когда углы Эйлера равны нулю, подвижные оси совпадают с неподвижными. Чтобы определить положение тела, соответствующее заданным углам Эйлера, производим следующие действия. Сначала подвижные оси, а значит и тело, поворачиваем на угол 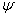 вокруг оси
вокруг оси 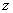 . При этом оси
. При этом оси 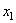 и
и 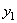 отойдут от осей
отойдут от осей 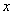 и
и 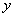 в горизонтальной плоскости и ось
в горизонтальной плоскости и ось 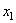 займёт положение
займёт положение  (рис.20). Затем тело вращаем вокруг нового положения оси
(рис.20). Затем тело вращаем вокруг нового положения оси 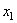 (прямой
(прямой  ) на угол
) на угол 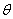 . Ось
. Ось 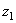 отойдёт от оси
отойдёт от оси 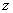 на этот угол
на этот угол 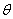 , а ось
, а ось 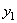 приподнимется над горизонтальной плоскостью. Наконец, тело (и подвижные оси) вращаем вокруг нового положения оси
приподнимется над горизонтальной плоскостью. Наконец, тело (и подвижные оси) вращаем вокруг нового положения оси 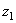 на угол
на угол  . Ось
. Ось 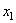 отойдёт от положения
отойдёт от положения 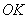 в наклонной плоскости, перпендикулярной оси
в наклонной плоскости, перпендикулярной оси 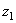 . Это положение тела и будет соответствовать углам Эйлера (на рисунке само тело не показано).
. Это положение тела и будет соответствовать углам Эйлера (на рисунке само тело не показано).
Линия пересечения неподвижной плоскости 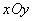 и подвижной
и подвижной 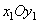 , прямая
, прямая 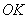 , называется линией узлов. Угол
, называется линией узлов. Угол 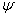 называется углом прецессии, угол
называется углом прецессии, угол 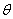 – углом нутации, угол
– углом нутации, угол  – углом собственного вращения. Эти названия углов пришли из теории гироскопов.
– углом собственного вращения. Эти названия углов пришли из теории гироскопов.
При движении тела углы Эйлера изменяются по определённым законам 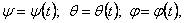 которые называются уравнениями вращения.
которые называются уравнениями вращения.
На примере вращающегося волчка можно лучше разобраться в этих углах Эйлера (рис.21). Ось волчка 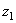 описывает конус вокруг неподвижной оси
описывает конус вокруг неподвижной оси 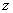 . Это вращение определяется углом
. Это вращение определяется углом 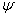 (говорят: волчок совершает прецессию). Отклонение оси волчка от вертикали – угол нутации
(говорят: волчок совершает прецессию). Отклонение оси волчка от вертикали – угол нутации 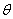 .
.
А вращение волчка вокруг своей оси 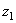 , определяемое углом
, определяемое углом  – собственное вращение.
– собственное вращение.
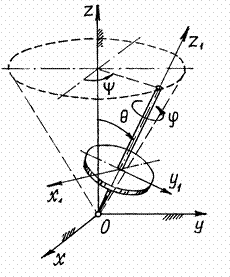
Рис.21
2) Теорема Даламбера – Эйлера. Мгновенная ось вращения.
Проведём в теле сферическую поверхность произвольного радиуса с центром в неподвижной точке  (рис.22).
(рис.22).
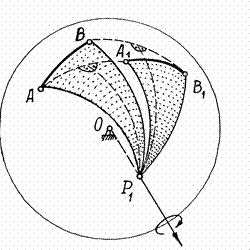
Рис.22
Покажем у тела какие-нибудь две точки  и
и 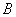 , расположенные на этой сфере. Соединим их по сфере дугой наибольшего радиуса (кратчайшее расстояние между точками). Переместим тело в новое положение. Точки, а значит и дуга, займут положение
, расположенные на этой сфере. Соединим их по сфере дугой наибольшего радиуса (кратчайшее расстояние между точками). Переместим тело в новое положение. Точки, а значит и дуга, займут положение 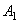 и
и 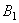 . Соединим точки
. Соединим точки 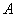 и
и 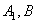 и
и 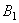 дугами большого радиуса
дугами большого радиуса 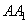 и
и 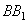 . Посередине этих дуг проведём им перпендикулярные дуги и найдём их точку пересечения
. Посередине этих дуг проведём им перпендикулярные дуги и найдём их точку пересечения 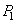 . Соединим эту точку
. Соединим эту точку 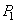 с точками
с точками 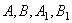 . Получим два сферических треугольника
. Получим два сферических треугольника 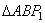 и
и 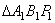 , расположенных на этой сфере. Эти два треугольника равны, как треугольники с равными сторонами (
, расположенных на этой сфере. Эти два треугольника равны, как треугольники с равными сторонами ( 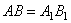 , а
, а 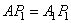 и
и 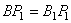 – как дуги равноудалённые от перпендикуляров). Так как эти два треугольника расположены на одной сфере и имеют общую вершину
– как дуги равноудалённые от перпендикуляров). Так как эти два треугольника расположены на одной сфере и имеют общую вершину 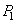 , то их можно совместить поворотом сферы, а значит и тела, вокруг прямой
, то их можно совместить поворотом сферы, а значит и тела, вокруг прямой 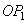 .
.
Поэтому можно сделать вывод, что тело с одной неподвижной точкой можно переместить из одного положения в другое поворотом вокруг некоторой оси, проходящей через неподвижную точку 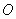 .Это утверждение – есть теорема Даламбера-Эйлера.
.Это утверждение – есть теорема Даламбера-Эйлера.
|
Конечно, такое перемещение не является истинным движением тела. На самом деле тело переходило из первого положения в другое каким-то другим, наверное более сложным путём. Но, если время 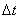 такого перехода мало, то это перемещение будет близко к действительному. А при
такого перехода мало, то это перемещение будет близко к действительному. А при 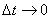 можно предположить, что для данного момента времени тело поворачивается вокруг некоторой оси Р, проходящей через неподвижную точку
можно предположить, что для данного момента времени тело поворачивается вокруг некоторой оси Р, проходящей через неподвижную точку 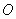 , вращаясь вокруг неё с угловой скоростью
, вращаясь вокруг неё с угловой скоростью 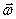 . Конечно, для каждого другого момента времени эта ось расположена иначе. Поэтому ось
. Конечно, для каждого другого момента времени эта ось расположена иначе. Поэтому ось 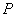 называют мгновенной осью вращения,а угловую скорость
называют мгновенной осью вращения,а угловую скорость 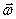 – мгновенной угловой скоростью, вектор которой направлен по оси.
– мгновенной угловой скоростью, вектор которой направлен по оси.
|
3) Скорость точек тела.
По теореме Даламбера-Эйлера за малое время 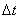 движение тела можно представить как вращение вокруг неподвижной оси
движение тела можно представить как вращение вокруг неподвижной оси 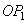 с некоторой угловой скоростью
с некоторой угловой скоростью 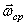 (рис.23).
(рис.23).
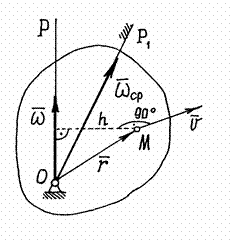
Рис.23
Тогда скорость точки 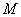 :
: 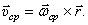 В пределе, при
В пределе, при 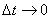 , угловая скорость
, угловая скорость 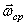 будет приближаться к мгновенной угловой скорости
будет приближаться к мгновенной угловой скорости 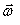 , направленной по мгновенной оси вращения
, направленной по мгновенной оси вращения 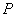 , а скорость точки
, а скорость точки 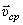 - к истинному значению:
- к истинному значению:
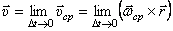
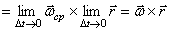 .
.
Но таким же образом находится скорость точки при вращении тела вокруг оси, по которой направлен вектор 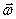 , в нашем случае – по мгновенной оси вращения
, в нашем случае – по мгновенной оси вращения 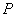 . Поэтому скорость точки можно определить как скорость её при вращении тела вокруг мгновенной оси
. Поэтому скорость точки можно определить как скорость её при вращении тела вокруг мгновенной оси 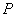 . Величина скорости
. Величина скорости 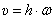 (рис.23).
(рис.23).
|
Определение скоростей точек тела значительно упрощается, если известна мгновенная ось вращения 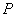 . Иногда её можно найти, если удастся обнаружить у тела хотя бы ещё одну точку, кроме
. Иногда её можно найти, если удастся обнаружить у тела хотя бы ещё одну точку, кроме 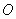 , скорость которой в данный момент равна нулю, и провести ось
, скорость которой в данный момент равна нулю, и провести ось 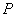 из неподвижной точки Очерез эту точку. Так как мгновенная ось вращения – геометрическое место точек, скорости которых равны нулю в данный момент времени.
из неподвижной точки Очерез эту точку. Так как мгновенная ось вращения – геометрическое место точек, скорости которых равны нулю в данный момент времени.
Пример 6. Водило  , вращаясь вокруг вертикальной оси
, вращаясь вокруг вертикальной оси  с угловой скоростью
с угловой скоростью  , заставляет диск радиуса
, заставляет диск радиуса  кататься по горизонтальной плоскости (рис.24).
кататься по горизонтальной плоскости (рис.24).
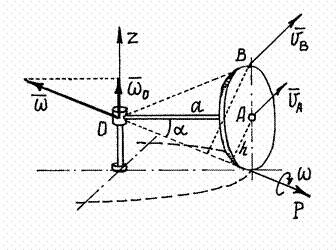
Рис.24
|
Если представить диск как основание конуса с вершиной в неподвижной точке  , то движение диска можно назвать вращением вокруг этой неподвижной точки
, то движение диска можно назвать вращением вокруг этой неподвижной точки  .
.
Так как скорость точки касания диска с плоскостью равна нулю, то мгновенная ось вращения 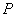 проходит через эту точку. И вектор мгновенной угловой скорости
проходит через эту точку. И вектор мгновенной угловой скорости 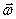 будет направлен по этой оси.
будет направлен по этой оси.
Точка 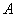 вместе с водилом
вместе с водилом 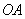 вращается вокруг оси
вращается вокруг оси 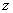 . Поэтому её скорость
. Поэтому её скорость 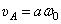 (рис.24). Эта скорость определяет направление вращения диска вокруг оси
(рис.24). Эта скорость определяет направление вращения диска вокруг оси 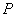 и направление вектора
и направление вектора 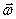 . Величина угловой скорости
. Величина угловой скорости 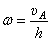 (h – расстояние от
(h – расстояние от 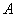 до оси
до оси 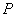 ). Теперь можно найти скорость любой точки диска, рассматривая его движение как вращение вокруг оси
). Теперь можно найти скорость любой точки диска, рассматривая его движение как вращение вокруг оси 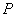 . Так, например, скорость точки
. Так, например, скорость точки 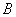 :
: 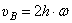 . Так как
. Так как 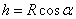 и
и 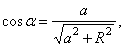
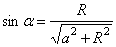 , то
, то 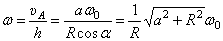 и
и 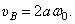
4) Ускорение точек тела.
Сначала определим угловое ускорение тела 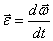 . При движении тела вектор угловой скорости
. При движении тела вектор угловой скорости  изменяется и по величине, и по направлению. Точка расположенная на его конце будет двигаться по некоторой траектории со скоростью
изменяется и по величине, и по направлению. Точка расположенная на его конце будет двигаться по некоторой траектории со скоростью  (рис.25).
(рис.25).
Рис.25
Если рассматривать вектор 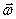 как радиус-вектор этой точки, то
как радиус-вектор этой точки, то 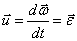 .
.
Итак. Угловое ускорение тела можно определить как скорость точки, расположенной на конце вектора угловой скорости:
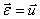 .
.
Этот результат называется теоремой Резаля.
Теперь обратимся к определению ускорения точек. Ускорение какой-либо точки 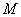 тела
тела
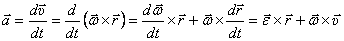 ,
,
есть сумма двух векторов.
Первый вектор 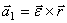 . Модуль его
. Модуль его 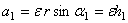 , где h1 – расстояние от точки
, где h1 – расстояние от точки 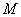 до вектора
до вектора  . Направлен он перпендикулярно
. Направлен он перпендикулярно 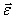 и
и 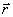 . Но таким же способом определяется касательное ускорение. Поэтому первую составляющую ускорения определяют как касательное ускорение, предполагая, что тело вращается вокруг оси, совпадающей с вектором
. Но таким же способом определяется касательное ускорение. Поэтому первую составляющую ускорения определяют как касательное ускорение, предполагая, что тело вращается вокруг оси, совпадающей с вектором 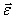 . И обозначается этот вектор ускорения так
. И обозначается этот вектор ускорения так
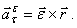
Второй вектор 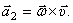 Модуль его
Модуль его 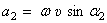 , но
, но 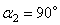 , т.к. векторы
, т.к. векторы 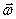 и
и 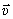 перпендикулярны друг другу.
перпендикулярны друг другу.
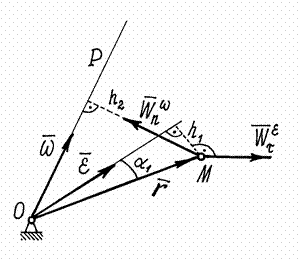
Рис.26
Значит 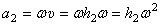 , где h2 – расстояние от точки М до мгновенной оси
, где h2 – расстояние от точки М до мгновенной оси 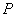 , до вектора
, до вектора 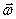 .
.
Направлен вектор 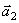 перпендикулярно
перпендикулярно 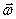 и
и 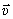 , т.е. так же как вектор нормального ускорения при вращении вокруг оси
, т.е. так же как вектор нормального ускорения при вращении вокруг оси 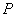 , или вектора
, или вектора 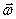 . Поэтому этот вектор ускорения и обозначают, соответственно, так:
. Поэтому этот вектор ускорения и обозначают, соответственно, так:
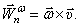
Итак, ускорение точек тела, вращающегося вокруг неподвижной точки, определяется как сумма двух ускорений:
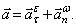
Этот результат называется теоремой Ривальса.
Заметим, что в общем случае векторы 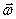 и
и 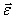 не совпадают и угол между
не совпадают и угол между 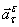 и
и 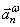 не равен
не равен 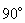 , векторы не перпендикулярны друг другу, как это было при вращении тела вокруг неподвижной оси.
, векторы не перпендикулярны друг другу, как это было при вращении тела вокруг неподвижной оси.
Пример 7. Продолжим исследование движения диска (пример 6). Модуль угловой скорости 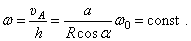 Значит вектор
Значит вектор 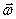 вместе с осью
вместе с осью 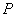 , которая всегда проходит через точку касания диска с плоскостью, вращается вокруг оси
, которая всегда проходит через точку касания диска с плоскостью, вращается вокруг оси 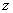 и описывает конус. Точка М на конце вектора
и описывает конус. Точка М на конце вектора 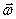 движется по окружности радиуса
движется по окружности радиуса 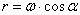 с угловой скоростью
с угловой скоростью 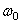 . Поэтому угловое ускорение диска
. Поэтому угловое ускорение диска 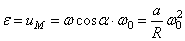 .
.
Откладывается вектор 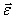 из неподвижной точки О. Направлен он, как скорость
из неподвижной точки О. Направлен он, как скорость 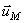 , перпендикулярно водилу
, перпендикулярно водилу 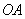 , параллельно оси х (рис. 27).
, параллельно оси х (рис. 27).
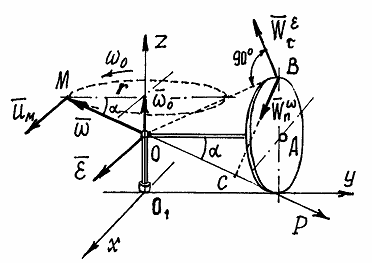
Рис.27
Найдём ускорение точки В.
Ускорение 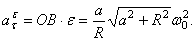 Направлен вектор
Направлен вектор 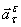 перпендикулярно
перпендикулярно 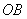 и расположен в плоскости
и расположен в плоскости 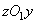 .
.
Ускорение 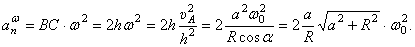 Вектор
Вектор 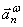 направлен по
направлен по  , перпендикулярно мгновенной оси
, перпендикулярно мгновенной оси 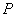 . Модуль вектора
. Модуль вектора 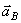 найдём с помощью проекций на оси
найдём с помощью проекций на оси 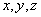 :
:
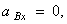
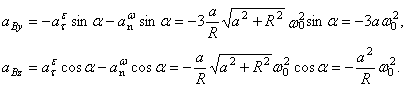
Значит 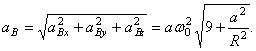
Дата добавления: 2015-06-17; просмотров: 2609;
