Мгновенный центр ускорений.

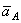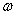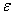При непоступательном движении плоской фигуры у нее в каждый момент времени имеется точка Q, ускорение которой равно нулю. Эта точка называется мгновенным центром ускорений. Определяется положение центра Q, если известны ускорение какой-нибудь точки А фигуры и величины и , следующим путем:

1) находим значение угла 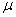, из формулы ;

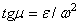2) от точки А под углом 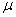, к вектору 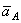проводим прямую АЕ (рис.45);

при этом прямая АЕ должна быть отклонена от 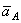в сторону вращения фигуры, если вращение является ускоренным, и против вращения, если оно является замедленным, т. е. в сторону направления углового ускорения ;

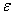3) откладываем вдоль линии АЕ отрезок AQ, равный

.

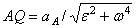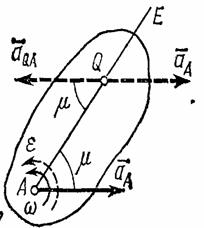
Рис.45

Построенная таким путем точка Q и будет мгно­венным центром ускорений. В самом деле, известно что

,

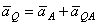где численно 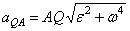. Подставляя сюда значение AQ находим, что 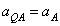. Кроме того, вектор 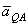должен образовывать с ли­нией AQ угол 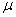, следовательно, вектор 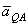параллелен 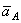, но направлен в про­тивоположную сторону. Поэтому 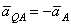и .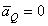

Если точку Q выбрать за полюс, то так как 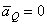, ускорение любой точки М тела, будет

.

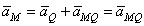При этом численно

.

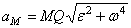Следовательно, ускорения точек плоской фигуры определяются в данный мо­мент времени так, как если бы движение фигуры, было вращением вокруг мгновенного центра ускорений Q. При этом

,

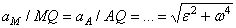т.е. ускорения точек плоской фигуры пропорциональны их расстояниям от мгно­венного центра ускорений. Картина распределения ускорений точек плоской фигуры в данный момент времени показана на рис.46.

Следует иметь в виду, что положения мгновенного центра скоростей Р и мгно­венного центра ускорений Q в данный момент времени не совпадают. Например, если колесо катится по прямолинейному рельсу (см. рис.47), причем скорость его центра С постоянна ( 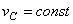), то мгновенный центр скоростей находится в точ­ке Р ( 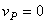), но при этом, как было показано 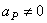; следовательно, точка Р не является одновременно мгновенным центром ускорений.

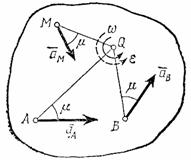
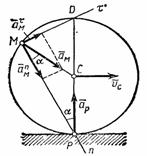
Рис.46 Рис.47

Мгновенный центр ускорений в этом случае находится, очевидно, в точке С, так как она дви­жется равномерно и прямолинейно и 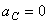. Центры скоростей и ускорений сов­падают тогда, когда фигура (тело) вращается вокруг неподвижной оси.

Понятием о мгновенном центре ускорений удобно пользоваться при решении некоторых задач.