Другий закон Ньютона і дві задачі динаміки
Динаміка розв’язує дві взаємно-обернені задачі:
– по відомим траєкторії і закону руху знаходять можливі сили, що діють на тіло;
– по заданим силам знаходять траєкторію і закон руху тіла.
Розглянемо першу задачу.
Задано: траєкторія графічно (рис.3.2), або аналітично і закон руху будь-яким способом, наприклад, звичайним S=S(t).
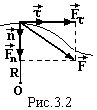 Знайти: силу F-?
Знайти: силу F-?
 По траєкторії, знаходять одиничні вектори
По траєкторії, знаходять одиничні вектори 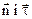 , а також радіус R її кривизни. Тоді згідно з другим законом Ньютона
, а також радіус R її кривизни. Тоді згідно з другим законом Ньютона 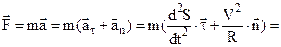
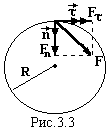

 Якщо рух тіла по колу радіусом R (рис.3.3) заданий кутовою координатою, яка змінюється по закону φ = φ(t), то сила
Якщо рух тіла по колу радіусом R (рис.3.3) заданий кутовою координатою, яка змінюється по закону φ = φ(t), то сила
знаходиться так: 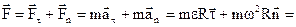
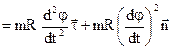
Сила  направлена перпендикулярно до дотичної, тобто до центра кривизни траєкторії. Тому її ще називають доцентровою силою. Як бачимо, перша задача динаміки розв’язується шляхом диференціювання.
направлена перпендикулярно до дотичної, тобто до центра кривизни траєкторії. Тому її ще називають доцентровою силою. Як бачимо, перша задача динаміки розв’язується шляхом диференціювання.
Розглянемо другу задачу динаміки.
Задано: закон зміни сили  як функцію часу, швидкості, шляху.
як функцію часу, швидкості, шляху.
Знайти: закон руху S = S(t).
Вона розв’язується інтегруванням. Окрім сили повинні бути задані і початкові умови, так як під дією однієї і тієї ж сили, але при різних початкових умовах, характер руху тіла різний. Наприклад, рух тіла під дією сили тяжіння з різними початковими умовами може бути:
вільне падіння; рух тіла, кинутого вертикально вгору; рух тіла, кинутого під кутом до горизонту; рух по колу – штучний супутник Землі.
Так як в загальному вигляді ця задача не розв’язується, розглянемо два приклади.
Приклад 1. Тіло масою m рухається під дією сили, яка не змінює напрямку і пропорційна часу F = k∙t. Початкові умови:
при t = 0 V = Vo, S = So.
Так як сила не змінює напрямку, тіло буде рухатись по прямій лінії. Знайдемо закон зміни швидкості і шляху від часу. Записуємо другий закон Ньютона

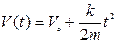 За означенням (2.2) швидкість
За означенням (2.2) швидкість 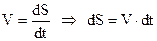
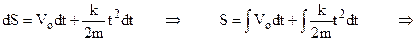
 .
.
Приклад 2.Тіло масою m рухається прямолінійно під дією сили опору, яка пропорційна швидкості  . Початкові умови:
. Початкові умови:
при t = 0 V = Vo, S = So.
Знайдемо закон зміни швидкості і шляху від часу. Записуємо другий закон Ньютона
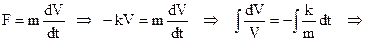
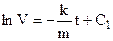 . Константу інтегрування С1 знайдемо, підставивши початкові умови. Одержимо, С1=lnVo. Отже,
. Константу інтегрування С1 знайдемо, підставивши початкові умови. Одержимо, С1=lnVo. Отже, 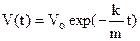 .
.

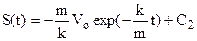 . Підстановка початкових умов дає
. Підстановка початкових умов дає
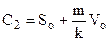 Отже,
Отже,  , або
, або
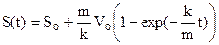 . Намалюємо графіки V(t) і S(t).
. Намалюємо графіки V(t) і S(t).
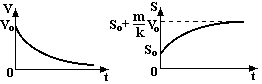
Дата добавления: 2015-06-17; просмотров: 1169;
