Рух тіла по колу. Кутова швидкість та кутове прискорення. Аналогія поступального і обертального рухів
При вивченні обертального руху зручніше характеризувати його
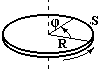 не лінійними параметрами (шлях, швидкість, лінійне прискорення), а кутовими: кутом повороту, кутовою швидкістю, кутовим прискоренням. Зручність зумовлена тим, що для різних точок тіла кутові характеристики однакові на відміну від лінійних.
не лінійними параметрами (шлях, швидкість, лінійне прискорення), а кутовими: кутом повороту, кутовою швидкістю, кутовим прискоренням. Зручність зумовлена тим, що для різних точок тіла кутові характеристики однакові на відміну від лінійних.
Дамо означення кутовим характеристикам обертального руху.
Кут повороту φ – це кут, на який повертається радіус-вектор будь-якої точки тіла. Вимірюється в радіанах. Довжина дуги (шлях S) зв’язана з кутом повороту (кутовою координатою) через радіус
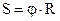 . (2.10)
. (2.10)
Кутова швидкість ω - це границя відношення кута повороту ∆φ до проміжку часу ∆t, за який цей поворот здійснений, при умові, що ∆t зменшується до нуля, тобто перша похідна від кута повороту за часом
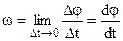 . (2.11)
. (2.11)
Кут повороту є величина псевдоскалярна, так як його знак змінюється при переході від правої системи координат до лівої.
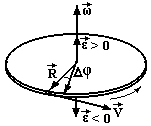
 Тому кутову швидкість прийнято вважати вектором (рис.2.4), направленим вздовж осі обертання у відповідності з правилом правого гвинта: якщо обертати гвинт з правою різьбою разом з тілом, то поступальний рух гвинта вкаже напрямок вектора кутової швидкості. З кінця цього вектора обертання тіла видно проти годинникової стрілки. Вимірюється кутова швидкість в рад/с.
Тому кутову швидкість прийнято вважати вектором (рис.2.4), направленим вздовж осі обертання у відповідності з правилом правого гвинта: якщо обертати гвинт з правою різьбою разом з тілом, то поступальний рух гвинта вкаже напрямок вектора кутової швидкості. З кінця цього вектора обертання тіла видно проти годинникової стрілки. Вимірюється кутова швидкість в рад/с.
Встановимо зв’язок між кутовою та лінійною швидкостями, скориставшись означеннями швидкостей (2.2), (2.11) і співвідношенням (2.10).
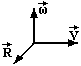
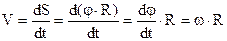 (2.12)
(2.12)
Вектори 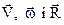 , як видно із рис.2.4, взаємно-перпендикулярні. Тому рівняння (2.12) записують у векторній формі через векторний добуток
, як видно із рис.2.4, взаємно-перпендикулярні. Тому рівняння (2.12) записують у векторній формі через векторний добуток
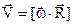 . (2.13)
. (2.13)
Кутове прискорення 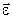 -це границя відношення зміни кутової швидкості
-це границя відношення зміни кутової швидкості 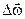 до проміжку часу ∆t, за який ця зміна відбулася, при умові, що ∆t → 0, тобто це перша похідна від кутової швидкості за часом.
до проміжку часу ∆t, за який ця зміна відбулася, при умові, що ∆t → 0, тобто це перша похідна від кутової швидкості за часом.
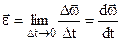 . (2.14)
. (2.14)
Так як вектор 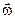 направлений по осі обертання, то і вектор
направлений по осі обертання, то і вектор 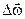 , а отже і вектор кутового прискорення
, а отже і вектор кутового прискорення 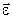 теж направлений вздовж закріпленої осі обертання (рис.2.4). У випадку прискореного руху він співпадає з напрямком кутової швидкості і протилежний їй при сповільненому русі. Вимірюється кутове прискорення в рад/с2.
теж направлений вздовж закріпленої осі обертання (рис.2.4). У випадку прискореного руху він співпадає з напрямком кутової швидкості і протилежний їй при сповільненому русі. Вимірюється кутове прискорення в рад/с2.
Встановимо зв’язок між лінійним та кутовим прискореннями, скориставшись (2.5), (2.13), (2.14) і (2.3),
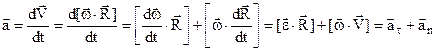 .
.
Тут 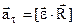 , (2.15)
, (2.15)
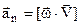 (2.16)
(2.16)
відомі нам дотичне і нормальне прискорення.
Приклад. Одержимо рівняння рівнозмінного обертального руху. Для нього 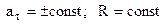 (див. п.2.6, випадок 5). Це еквівалентно співвідношенням
(див. п.2.6, випадок 5). Це еквівалентно співвідношенням 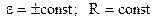 , тобто
, тобто 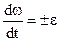 . Інтегруємо останнє рівняння з початковими умовами: при t = 0 ω = ωo, φ = φo. Одержимо рівняння
. Інтегруємо останнє рівняння з початковими умовами: при t = 0 ω = ωo, φ = φo. Одержимо рівняння
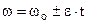 (2.17)
(2.17)
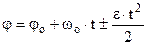 , (2.18)
, (2.18)
які аналогічні рівнянням прямолінійного рівнозмінного руху
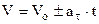
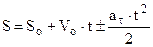 .
.
Таким чином, між поступальним і обертальним рухами існує аналогія величин 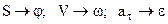 і формул. Так у поступальному русі відома формула
і формул. Так у поступальному русі відома формула 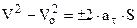 . Замінивши відповідні величини, одержуємо для рівнозмінного обертального руху
. Замінивши відповідні величини, одержуємо для рівнозмінного обертального руху
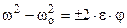 .
.
Дата добавления: 2015-06-17; просмотров: 3981;
