Аналогічно для поступального руху

Вступ

Вирішальний вплив на розвиток продуктивних сил суспільства має спосіб отримання механічної енергії для виконання роботи. Перехід на парові двигуни для привода робочих машин обумовив стрімке зростання виробництва у XVIII – XIX ст. А вже XX ст. стало віком електрики, бо основним джерелом механічної енергії стали більш досконалі електричні двигуни. Так як електропривод (ЕП) народився в надрах віку пару, то на перших порах електричним двигуном замінювали парову машину для приводу трансмісії цілого цеху. Основним недоліком такого електропривода було збереження громіздкої механічної трансмісії, за допомогою якої механічна енергія від електродвигуна розподілялась до всіх робочих машин та їх механізмів, рис.В.1. Але цей, на перший погляд простий перехід, дозволив централізовано виробляти електроенергію на електростанціях, які можна було зручно розташовувати біля родовищ корисних копалин чи на річках та розподіляти електроенергію за допомогою електромережі між споживачами.

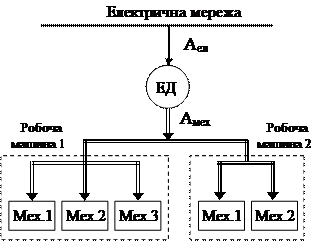Рис.В.1. А_ел – електрична енергія, А_мех – механічна енергія,

ЕД – електричний двигун, Мех. – механізм.

Наступним етапом розвитку електропривода стало встановлення на кожній робочій машині окремого електродвигуна, рис.В.2. Розподіл механічної енергії до механізмів робочої машини як і раніше здійснюється механічною трансмісією, але така схема потребувала вже нового підходу до конструювання робочих машин і звільнила цехи від громіздкої механічної трансмісії. Проте електроприводи на рис.В.1 і В.2 виконують однакові функції – лише перетворення електричної енергії у механічну для приводу групи механізмів, тому ці схеми представляють один вид електропривода, який називається груповим. Особливістю групового електропривода є неможливість керування технологічним процесом за допомогою системи керування електроприводом (СКЕП), так як пуск, зупинка, зміна величини та напрямку швидкості робочих органів механізмів здійснюється за допомогою механічних засобів: коробок передач, фрикційних механізмів, муфт тощо. Електропривод за рис.В.1 зараз не використовується, а за рис.В.2 ще експлуатується, особливо в металообробці та текстильній промисловості.

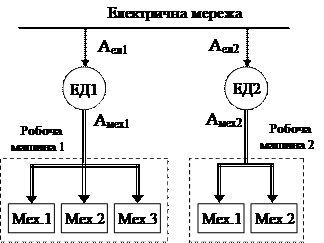Рис.В.2.

Складна кінематика та високі вимоги до виготовлення деталей механічної трансмісії, необхідність автоматизації виробництва обумовило заміну групового електропривода індивідуальним, коли кожен механізм має один або декілька двигунів, рис.В.3.

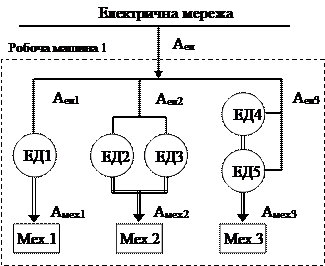Рис.В.3.

В останньому випадку електропривод називається багатодвигунним, як механізмів 2 та 3. Перехід на індивідуальний електропривод дає якісну зміну, бо крім функції перетворення електричної енергії у механічну він може виконувати функцію керування рухом робочого органу механізму - пуск, зупинка, зміна швидкості, реверс тощо. При цьому електропривод разом із механізмом зливаються в єдину електромеханічну систему, що дозволяє оптимізувати її роботу та взаємно пов’язати з ходом технологічного процесу. Це обумовлює й характерну тенденцію розвитку електропривода – спрощення кінематики та ускладнення системи керування.

Таким чином сучасний ЕП є індивідуальним і виконує дві основні функції:

1) перетворення електричної енергії у механічну;

2) керування рухом робочого органу механізму.

Згідно до стандарту ГОСТ 16593-79 електроприводом називається електромеханічна система, яка складається з електродвигунного, перетворювального, передавального та керуючого пристроїв, і яка призначена для приводу в рух робочих органів машини й керування цим рухом. Згідно наведеного, функціональну схему електропривода представлено на рис.В4.

Рис.В.4.

Для виконання своїх функцій електропривод підключено до електричної мережі, із якої він споживає електроенергію. Якщо електропривод живиться не від мережі, а від окремого джерела електроенергії (акумуляторна чи сонячна батарея, дизель-генератор тощо), то він називається автономним.

Електродвигунний пристрій (ЕДП) – це основний елемент електропривода. В якості ЕДП виступають рушії різних типів (двигуни постійного струму, асинхронні та синхронні двигуни змінного струму, лінійні та дугостаторні двигуни, вентильні та крокові двигуни тощо), які перетворюють електричну енергію в механічну. (В окремих режимах роботи згідно зворотності електричних машин ЕП може здійснювати зворотне перетворення механічної енергії від механізму в електричну енергію та віддавати її до мережі).

Перетворювальний пристрій (ПП) керує потоком електричної енергії, яка поступає від електромережі до електродвигунного пристрою, із метою зміни режиму роботи останнього. ПП може бути простим, у вигляді силових перемикачів, або складним, у вигляді керованих випрямлячів, перетворювачів частоти, інверторів, широтно-імпульсних перетворювачів тощо. ПП складає силову електричну частину системи керування електроприводом.

Передавальний пристрій (ПДП) необхідний для передачі механічної енергії від двигуна до механізму. Це редуктори, ремінні, рейкові та кривошипно-шатунні передачі, передачі “гвинт-гайка” тощо. Якщо передавальний пристрій відсутній, то електропривод називається безпосереднім.

Керуючий пристрій (КП) призначено для керування електродвигунним пристроєм за допомогою перетворювального, а також збору та обробки інформації. Він являє собою несилову інформаційну частину системи керування електроприводом. КП у залежності від складності електропривода може бути реалізовано за допомогою кнопок, реле, командоапаратів чи інтегральних мікросхем, мікропроцесорів, керуючих ЕОМ тощо.

За рахунок керованої механічної енергії, отриманої від електропривода, робочий орган механізму (кабіна ліфта, східці ескалатора, шпиндель станка, гак крана, маніпулятор робота тощо) виконує необхідний технологічний рух. Основними координатами цього механічного руху є кутова чи лінійна швидкість, момент чи зусилля, кутове чи лінійне положення, тому і системи керування електроприводів розділяються на три основні види:

1) керування швидкістю;

2) керування моментом (зусиллям);

3) керування положенням.

Електропривод є найбільшим споживачем електроенергії. Близько 2/3 всієї електроенергії світу споживає електропривод, тому важливими є питання енергозбереження, раціонального використання, підвищення ККД та мінімізації втрат у процесі роботи електропривода.

За час розвитку теорії електропривода (ТЕП) отримано надбання, які можна розділити на три групи:

1) загальна теорія, яка вивчає фізичні закономірності та методи розрахунку електропривода;

2) теорія окремих систем електропривода у залежності від технічної реалізації (частотний ЕП змінного струму, вентильний ЕП, тиристорний ЕП постійного струму тощо);

3) теорія застосування електропривода в окремих областях (ЕП прокатних станів, ЕП побутових машин, ЕП станків тощо).

Електропривод включає механічну частину, закони руху якої досліджуються методами теоретичної механіки, а властивості – прикладної механіки, теорії машин та механізмів. Електромеханічні перетворення енергії у двигуні описуються в теорії електричних машин. Керування потоком електричної енергії в електричній частині електропривода не можливе без знань законів теоретичної електротехніки та електроніки. Загальні методи аналізу та синтезу базуються на законах теорії автоматичного керування. Таким чином, для опанування теорією електропривода необхідні знання з вищевказаних базових дисциплін та із загальнотеоретичних дисциплін, як математика, фізика тощо

1.МЕХАНІКА ЕЛЕКТРОПРИВОДУ

1.1.Загальні відомості

Механічна частина електропривода – це рухомі маси двигуна (ротор) та передавального пристрою. З механічною частиною електропривода безпосередньо зв’язаний робочий орган (РО) механізму, який є об’єктом керування електропривода, рис. В.4. Хоча робочий орган механізму не входить до механічної частини електропривода, але його параметри (маса, момент інерції тощо) враховуються в математичному описі електропривода, тому при проектуванні електропривода потрібно розглядати кінематичну схему всієї електромеханічної системи. Кінематичні схеми дуже різноманітні, але вони мають загальні особливості, бо складаються з типових елементів, а саме - зв’язаних в один механічний ланцюг мас, що рухаються обертально чи поступально. При навантаженні елементи кінематичної схеми відповідно до закону Гука пружно деформуються, бо не є абсолютно жорсткими. Цей рух механічної частини електропривода описується законами теоретичної та прикладної механіки.

1.2. Розрахункові схеми та правила приведення параметрів

На кінематичній схемі елементи, які рухаються поступально, характеризуються масою m[кг], а ті, що рухаються обертально – моментом інерції J [кг·м²]. Кожен елемент, пов’язаний з наступним елементом невагомим механічним зв’язком, який характеризується жорсткістю c[Н/м], [Нм/рад].

Жорсткість – це величина зусилля чи моменту на одиницю деформації тіла. Чим більша жорсткість тіла, тим менше воно деформується. При поступальному русі на тіло діє пружне зусилля F₁₂=F₁- F₂ [Н], яке викликає деформацію DS=S₁-S₂ [м], рис.1.1. Жорсткість дорівнює відношенню c=F₁₂/DS [Н/м].

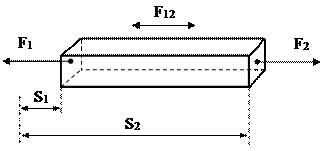Рис.1.1.

При обертальному русі на тіло діє пружний момент M₁₂=M₁- M₂ [Нм], який викликає деформацію Dj=j₁-j₂ [рад], рис.1.2. В цьому випадку жорсткість дорівнює c=M₁₂/Dj [Нм/рад].

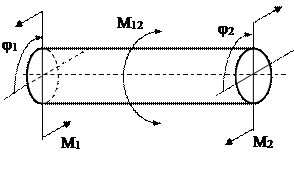
Рис.1.2.

Жорсткість залежить від геометричних розмірів тіла та матеріалу, із якого воно виготовлено. Для пружного стержня при його стисканні чи розтягуванні жорсткість визначається за наступною формулою

, [Н/м] (1.1)

де S – площа поперечного перерізу стержня, м² ;

E – модуль пружності матеріалу, Па ;

L – довжина стержня, м.

Для пружного валу при його скручуванні жорсткість визначається наступним чином

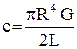, [Н·м] (1.2)

де G – модуль пружності скручування матеріалу, Па ;

R – радіус валу, м.

Величина, обернена до жорсткості, називається піддатливістю.

Найпершою задачею при проектуванні ЕП є складання на основі кінематичної схеми механічної частини електромеханічної системи розрахункової схеми та її спрощення до ступеня відповідно до вимог синтезу. Чим простіша розрахункова схема, тим простіший її математичний опис і відповідний регулятор, але при спрощенні не повинно якісно змінитися математична модель електромеханічної системи.

Кожен елемент кінематичної схеми характеризується жорсткістю, масою чи моментом інерції, сукупністю діючих на нього моментів чи сил, але має свою швидкість, тому для безпосереднього порівняння вказаних параметрів їх необхідно привести до однієї швидкості. Найчастіше приведення здійснюється до швидкості двигуна, але інколи - до лінійної швидкості робочого органу. В результаті приведення реальна кінематична схема замінюється енергетично еквівалентною розрахунковою. Найбільший вплив на рух мають елементи з найбільшою масою, як найбільш інерційні, та зв’язки з найменшою жорсткістю, бо призводять до коливань мас. Виділивши їх, можна спростити розрахункову схему й тим самим забезпечити меншу складність системи керування електроприводом.

На рис.1.3 представлено кінематичну схему підйомного механізму.

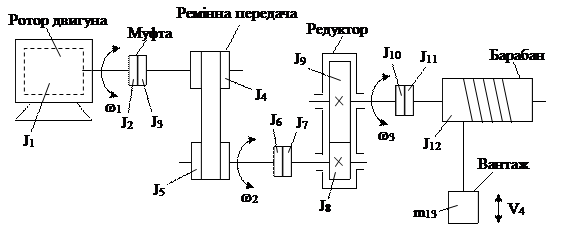Рис.1.3.

На основі цієї схеми спочатку складається попередня розрахункова схема, рис.1.4. Для цього вибирається швидкість, до якої буде здійснюватись приведення. У даному випадку - це швидкість двигуна w₁. Реальні елементи (двигун, редуктор тощо) на схемі зображуються прямокутниками, площа яких пропорційна їх моментам інерції (масам). Прямокутники з’єднуються невагомими зв’язками, довжина яких обернено пропорційна жорсткості валів чи каната. Елементи, які рухаються із швидкістю, відмінною від швидкості двигуна, позначаються з верхнім індексом “штрих”, що означає приведення параметрів до валу двигуна.

Рис.1.4.

Умовою приведення параметрів реальної схеми до розрахункової є виконання закону збереження енергії та елементарної роботи.

При приведенні моментів інерції та мас повинен виконуватися закон збереження кінетичної енергії. Для обертального руху при приведенні моменту інерції елемента, який рухається зі швидкістю w_i, до розрахункової швидкості w₁ повинна виконуватися умова

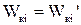, тобто 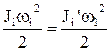, звідкіля

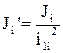, (1.3)

де 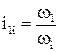- передаточне число від валу приведення до i-го валу.

Аналогічно для поступального руху 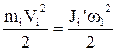, звідкіля

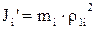, (1.4)

де 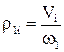- радіус приведення.

Для лінійних кінематичних зв’язків i_1i та r_1i є незмінними.

Переміщення та прискорення приводяться на основі відношення швидкостей елементів. Для обертального руху кутове переміщення j_i [рад] після приведення дорівнює

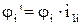, (1.5)

а кутове прискорення e_i [рад/с²]

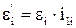. (1.6)

Для поступального руху лінійне переміщення S_i[м] після приведення визначається наступною формулою

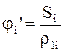, (1.7)

а лінійне прискорення a_i [м/с²]

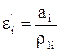. (1.8)

При приведенні жорсткостей повинен виконуватися закон збереження потенціальної енергії 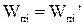. Для обертального руху

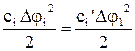, звідкіля

. (1.9)

Для поступального руху , звідкіля

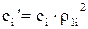. (1.10)

Приведення моментів та зусиль здійснюється за умови рівності елементарної роботи на можливих переміщеннях. Для обертального руху 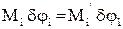, звідкіля приведений момент дорівнює

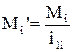. (1.11)

Для поступального руху 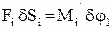, звідкіля знаходиться приведене зусилля

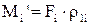. (1.12)

На основі аналізу числових значень приведених моментів інерції (мас) та жорсткостей виділяються найбільш суттєві, тобто найбільші приведені маси та найменші приведені жорсткості. На основі цього здійснюється спрощення. Декілька елементів схеми можна об’єднати в один. При цьому новий елемент буде характеризуватися еквівалентним (сумарним) моментом інерції та еквівалентною жорсткістю. При послідовному об’єднанні елементів еквівалентна жорсткість визначається за формулою

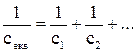, (1.13)

а при паралельному з’єднанні еквівалентна жорсткість дорівнює

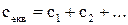(1.14)

Згідно вищенаведеного еквівалентний момент інерції дорівнює

,

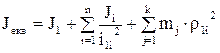де n – кількість приведених елементів, які рухаються обертально;

k – кількість приведених елементів, які рухаються поступально.

Нехай на попередній розрахунковій схемі, рис.1.4, найменшу жорсткість має ремінна передача та канат, тобто c₄^’ , c₁₂^’ , а найбільший момент інерції має двигун, барабан та вантаж, тобто J₁, J₁₂^’, J₁₃^’. Моменти інерцій елементів, які розділяються зв’язками з найменшими жорсткостями, об’єднуються

J_екв1 = J₁+ J₂+ J₃+ J₄ ;

J_екв2 = J₅^’+ J₆^’+ J₇^’+ J₈^’+ J₉^’+ J₁₀^’+ J₁₁^’+ J₁₂^’ ;

J_екв3 = J₁₃^’ .

Ці еквівалентні моменти інерції з’єднуються еквівалентними жорсткостями згідно (1.13), значення яких визначаються жорсткостями зв’язків, розташованих між найбільшими моментами інерції

c_екв2 = c₁₂^’ .

Після такого спрощення початкова розрахункова схема приймає наступний вигляд, рис.1.5.

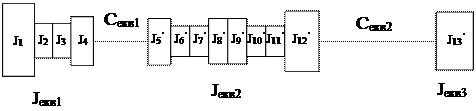Рис.1.5.

Тобто схема представляється трьома масами, з’єднаними двома пружними зв’язками. Якщо жорсткість с_екв2 набагато менша за с_екв1, то схему на рис.1.5 можна ще спростити, об'єднавши J_екв1 та J_екв2 , і отримати двомасову схему. На спрощених схемах еквівалентні маси зображуються колами, а жорсткості – у вигляді схематичних пружин.

При синтезі ЕП після спрощень найчастіше використовуються три розрахункові схеми:

1) Тримасова – для детального аналізу та якісного синтезу електромеханічних систем із двома суттєвими пружними зв’язками. Використовується найрідше, рис.1.6.

Рис.1.6.

2) Двомасова – найбільш адекватно відображує процеси більшості електромеханічних систем з одним суттєвим пружним зв’язком, рис.1.7.

Рис.1.7.

3) Одномасова – застосовується найчастіше для синтезу та аналізу електропривода та електромеханічних систем із високою жорсткістю зв’язків або коли жорсткістю зв’язків нехтують. Усі маси замінюються однією еквівалентною, рис.1.8.

Рис.1.8.

Рухомі елементи кінематичної схеми можуть мати паралельні ділянки, що характерно для багатодвигунних електроприводів. Еквівалента жорсткість обчислюється за формулою (1.14), рис.1.9.

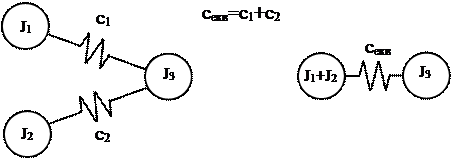Рис.1.9.

В реальних системах завжди є дисипативні сили, наприклад, сили внутрішнього в’язкого тертя, які призводять до поглинання енергії механічних коливань, обумовлених пружністю механічних зв’язків. На розрахункових схемах сили внутрішнього в’язкого тертя з коефіцієнтом тертя bпозначається механічним демпфером, який встановлюється паралельно пружному зв’язку, рис.1.10.

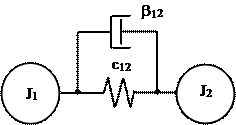Рис.1.10.

Сили внутрішнього тертя пропорційні швидкості деформації. Для обертального руху момент тертя дорівнює

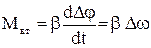, (1.15)

а для поступального руху сила тертя

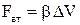. (1.16)

Приведення коефіцієнта в’язкого тертя (демпфірування) виконується на основі збереження енергії дисипації W_Д = W_Д^’ . Для обертального руху

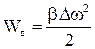, тому

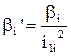. (1.17)

Аналогічно для поступального руху

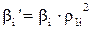. (1.18)

При послідовному з’єднанні елементів еквівалентний коефіцієнт тертя знаходиться аналогічно до (1.13)

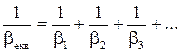, (1.19)

а при паралельному – до (1.14)

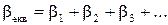(1.20)

З вищенаведеного розрахункова схема створюється за наступним алгоритмом:

1) Складається кінематична схема реальної системи;

2) Обчислюються реальні значення параметрів елементів кінематичної схеми: маси, моменти інерції, жорсткості тощо;

3) Визначається швидкість, до якої буде здійснюватися приведення параметрів (найчастіше - це швидкість двигуна);

4) Усі параметри приводяться до вибраної швидкості та складається попередня розрахункова схема;

5) По кількісних значеннях приведених параметрів визначаються суттєві жорсткості (найменші) та маси (найбільші);

6) На основі аналізу результату п’ятого пункту попередня розрахункова схема спрощується до необхідного ступеню, тобто до типової три-, дво-, чи одномасової схеми.

1.3. Типові статичні навантаження електропривода

На механічну частину електропривода діють:

1) електромагнітний момент двигуна, М;

2) статичний момент, створений робочими органами механізмів, М_с.

(В подальшому узагальнено розглядаються моменти сил, хоча всі приведені закономірності справедливі і для зусиль. Це пояснюється тим, що в електроприводі переважно використовуються електродвигуни обертального руху).

Статичний момент складається із суми моментів корисного навантаження SM_кн, необхідних для виконання роботи, та суми моментів втрат SDM, в тому числі механічних втрат у двигуні

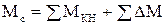. (1.21)

Моменти корисного навантаження в різних механізмах мають різний характер, але з них можна виділити типові. Крім того, основною координатою електропривода є швидкість, тому важливою є залежність статичного моменту від швидкості

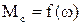або 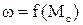. (1.22)

Ця залежність (1.22) називається механічною характеристикою механізму (двигун має також механічну характеристику). За своєю природою та за характером взаємодій з електроприводом усі статичні моменти розділяються на активні та реактивні.

1) Активний момент створюється зовнішніми, по відношенню до двигуна, джерелами енергії (сила вітру, сила тяжіння, потенціальна сила тощо) незалежно від напрямку руху електропривода. Сила тяжіння F вантажу механізму підйому завжди направлена до центру Землі, рис.1.11,а.

а) б)

Рис.1.11.

Статичний момент, який створює сила тяжіння, дорівнює

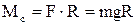(1.23)

де R – радіус барабана лебідки;

і пропорційно залежить від маси вантажу m, тому змінюється від нуля і до максимального значення M_сmax при зміні маси від нуля і до m_max. Цей статичний момент (1.23) не залежить від величини й напрямку швидкості, тому його механічна характеристика представляє собою пряму, розташовану в І-ому та ІV-ому квадранті (четверті) площини, рис.1.11, б. Якщо підйомний механізм врівноважено, наприклад, ліфт із противагою, то момент може змінюватись в більш широких межах, рис.1.12. В цьому випадку активний статичний момент дорівнює

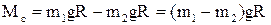, (1.24)

де m₂ – незмінна маса противаги.

Якщо m₁=0, то M_cmin= - m₂gR. При m₁=m₂ момент M_c=0, а при m₁=m_1max момент дорівнює максимальному додатному значенню M_cmax>0. Діапазон зміни статичного моменту вказано на рис.1.12.

2) Реактивний момент діє завжди проти напрямку руху, тому він змінює знак при зміні напрямку швидкості.

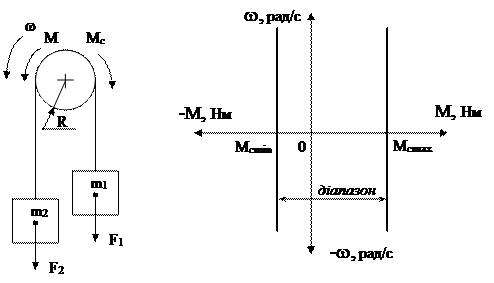
Рис.1.12.

Реактивний момент виникає як реакція на рушійний момент, створений двигуном або іншими активними силами, в тому числі силами інерції. За видом залежності від швидкості реактивний момент умовно розділяється на момент:

· сухого (кулонівського) тертя;

· в’язкого тертя;

· вентиляторного типу.

Момент сухого (кулонівського) тертя M_cо змінює стрибком своє значення на протилежне при зміні напрямку руху, рис.1.13.

Рис.1.13.

При цьому величина моменту не залежить від швидкості. На електропривод найчастіше діє саме момент сухого тертя, який описується наступною залежністю

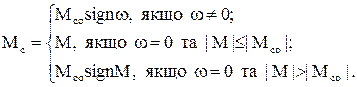(1.25)

В механізмах реальних момент сухого тертя має більш складний характер, так як момент зрушення може бути в декілька разів більшим за момент руху. Технологічні процеси обробки деталей на верстатах мають схожий вигляд, наприклад, момент різання на токарному верстаті, рис.1.14

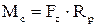. (1.26)

де F_z – зусилля різання;

R_р – радіус різання.

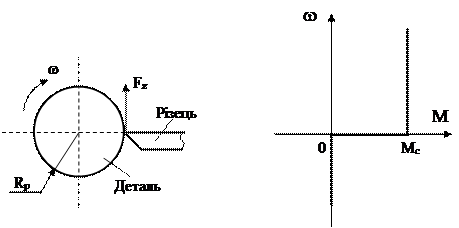Рис.1.14.

Момент в’язкого тертя лінійно залежить від швидкості, рис. 1.15

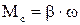, (1.27)

де b - коефіцієнт пропорційності.

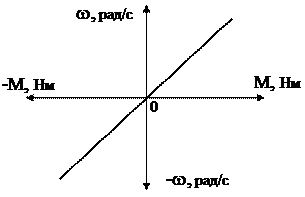Рис.1.15.

На практиці окремо цей вид моменту зустрічається рідко. Найчастіше він присутній у моменті реального тертя.

Момент вентиляторного типу залежить від квадрата швидкості й створюється струминними машинами (вентилятори, насоси), рис.1.16

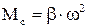. (1.28)

В механізмах цей момент найчастіше діє разом із моментом сухого тертя, рис.1.16. Деякі механізми, наприклад, відцентрові насоси, які працюють на протитиск, мають залежність від швидкості вище другої степені.

Рис.1.16. Ідеальний вентиляторний момент -1, вентиляторний

момент разом із моментом сухого тертя - 2.

Навантаження може бути періодичним. Найчастіше такий характер мають кривошипно-шатунні, кулісні та інші механізми, в яких радіус приведення залежить від кута повороту вала

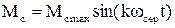, (1.29)

де w_сер – середня швидкість двигуна;

k – коефіцієнт повтору коливань навантаження;

t – час.

При обчисленні значення статичного моменту при приведенні моментів та сил до валу двигуна потрібно враховувати втрати в елементах кінематичного ланцюга (редуктори, ремінні передачі тощо). Найпростіше це зробити за допомогою сумарного ККД ланцюга, обчисленого на основі номінальних ККД цих елементів, вказаних у їх паспортних даних

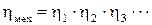(1.30)

Для точнішого визначення реального ККД і відповідно статичного моменту потрібно використовувати залежності ККД елементів від навантаження. Якщо знаки швидкості та статичного моменту протилежні, то при приведенні момент корисного навантаження ділиться на сумарний ККД

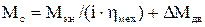, (1.31)

а якщо знаки моменту та швидкості співпадають, то множиться

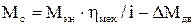, (1.32)

де DМ_дв – механічні втрати у двигуні.

Наприклад, для підйомного механізму активний статичний момент при підйомі вантажу M_c1 не співпадає за напрямком із швидкості, тому його значення більше моменту при опусканні вантажу M_c2 на величину сумарного моменту втрат DM, рис.1.17.

Рис.1.17.

Момент механічних втрат у двигуні DМ_дв складає всього 1¸5% від номінального моменту двигуна, тому при розрахунках він часто нехтується.

Реальний статичний момент конкретного ЕП для всіх його трьох типових розрахункових схем: три-, дво-, одномасової, рис.1.6 – рис.1.8, має одне незмінне значення

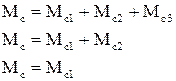(1.33)

але розподіляється між масами відповідно до реальних умов, наприклад, для тримасової схеми, рис.1.18.

Рис.1.18.

Важливим є завдання знаків моментів у формулах, представлених у скалярній формі. Момент двигуна М береться із знаком “+”, якщо його дія співпадає з напрямком швидкості w, та із знаком “-“, якщо не співпадає. Знак статичного моменту М_с, який діє проти напрямку швидкості, а це завжди реактивний момент та інколи активний, береться із знаком швидкості. Активний статичний момент, який є рушійним, тобто діє в напрямку швидкості, береться із знаком, протилежним до швидкості.

1.4. Рівняння руху механічної частини електропривода

Механічну частину ЕП можна представити системою твердих тіл, рух яких обмежений механічними зв’язками. Найбільш загальною формою запису диференційних рівнянь, які описують рух такої системи, є відоме рівняння Лагранжа 2-го роду

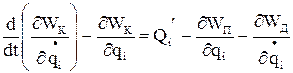, (1.34)

де W_К – кінетична енергії системи;

W_П – потенціальна енергії системи;

W_Д – енергія дисипації (розсіювання) системи;

Q_i` - узагальнена сила;

q_i – узагальнена координата;

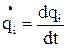- узагальнена швидкість;

i – кількість рівнянь, яка визначається степенем

вільності механічної системи.

В механічній частині електропривода кожна маса обертається на осі, тобто має одну степінь вільності, тому кількість рівнянь дорівнює кількості мас розрахункової схеми. Для обертального руху узагальненою координатою є кут повороту валу 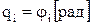, а узагальненою швидкістю – кутова швидкість валу 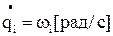. Відповідно для поступального руху це – лінійне переміщення 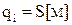та лінійна швидкість .

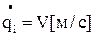1.4.1. Рівняння руху та структурна схема одномасової розрахункової схеми механічної частини електропривода

Розрахункова схема представляється однією масою із сумарним моментом інерції J, на яку діють момент двигуна М та статичний момент М_с . Під дією цих моментів маса рухається із швидкістю w , проходячи шлях j, рис.1.19.

Рис.1.19.

Для даної схеми складається рівняння Лагранжа згідно (1.34). Кінетична енергія дорівнює 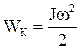, потенціальна - W_П=0, дисипаціі - W_Д=0. Похідна кінетичної енергії за кутом

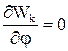(1.35)

та швидкістю

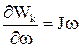. (1.36)

Узагальнена сила

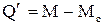. (1.37)