У рівняннях руху мас (1.46) і (1.50) момент

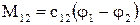(1.51)

є пружним моментом взаємодії двох мас, які рухаються. Похідна пружного моменту дорівнює

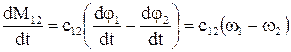. (1.52)

Наведені рівняння (1.46), (1.50), (1.52) описують рух електропривода, представленого двомасовою розрахунковою схемою

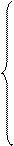
(1.53)

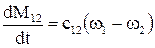
На основі рівнянь (1.53) складається структурна схема кожної ланки та системи в цілому, рис.1.25.

Рис.1.25.

Для систем керування положенням робочих органів механізмів потрібна інформація про переміщення мас j₁ та j₂ . Для цього рівняння (1.53) доповнюється інтеграторами (1.40) і набувають наступного вигляду

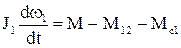
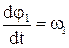(1.54)

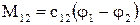
Структурна схема, яка відповідає рівнянням (1.54), представлена на рис.1.26.

Рис.1.26.

1.4.3. Рівняння руху та структурна схема двомасової розрахункової схеми механічної частини електропривода з урахуванням внутрішнього в’язкого тертя

Сили внутрішнього в’язкого тертя поглинають енергію коливань, обумовлену пружним зв’язком, тобто призводять до затухання коливань мас, проте величина цих сил незначна, тому вони суттєво на рух не впливають. Розрахункову схему механічної частини електропривода для цього випадку показано на рис.1.27.

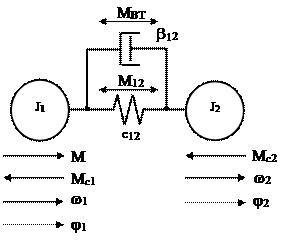Рис.1.27.

Кінетична енергія даної системи дорівнює 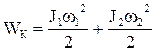, потенціальна - 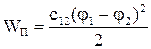, дисипаціі - 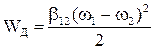. Після складання рівняння Лагранжа аналогічно (1.43)-(1.52) отримується система рівнянь (1.55), яка описує рух механічної частини електропривода згідно рис.1.27.

(1.55)

Останнє рівняння в системі (1.55) визначає момент внутрішнього в’язкого тертя М_ВТ. Відповідна структурна схема представлена на рис.1.28.

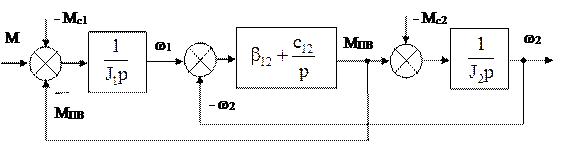
Рис.1.28.

Структурна схема реалізує реально існуючий у природі сумарний пружно-в’язкий момент М_пв=М₁₂+М_вт. Якщо для аналізу потрібно окремо виділити пружний момент М₁₂ та момент в’язкого тертя М_вт, то структурна схема представляється згідно рис.1.29.

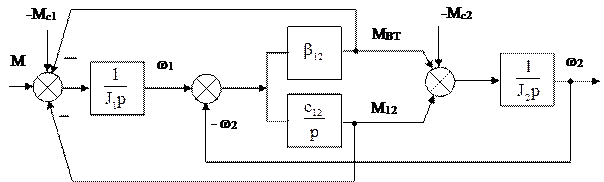Рис.1.29.

1.4.4. Рівняння руху та структурна схема двомасової розрахункової схеми механічної частини електропривода із зазором без врахування внутрішнього в’язкого тертя

Елементи механічної частини (шестерні редуктора, муфти тощо) можуть мати механічні зазори, обумовлені неточністю виготовлення деталей чи їх зносом. Зазор може бути вибраним (замкненим), якщо всі деталі щільно дотикаються одна до одної, або розімкненим, частково чи повністю. В останньому випадку окремі групи елементів рухаються незалежно. Наявність зазорів негативно впливає на рух механічної частини, так як призводить до ударів, інтенсивного зносу елементів та зниженню точності керування. При розробці розрахункової схеми зазори приводяться як переміщення до однієї швидкості згідно (1.5), (1.6). При описанні системи із зазором за допомогою рівняння Лагранжа обов’язково повинен враховуватися пружний зв’язок. Якщо пружність не враховується, то адекватне математичне описання потрібно розробляти на основі закону збереження імпульсу. Розрахункова схема представлена на рис.1.30.

Рис.1.30.

Наявність зазору Dj_з обумовлює нелінійність пружного моменту, рис.1.31

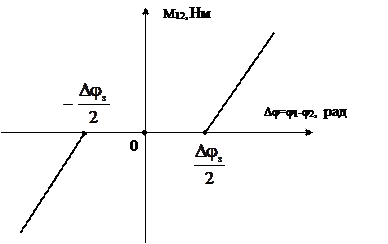Рис.1.31.

Усі інші рівняння аналогічні рівнянням двомасової схеми без зазору (1.54)

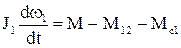
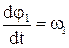(1.56)

На основі системи рівнянь (1.56), яка описує рух системи із зазором, складається відповідна структурна схема, рис.1.32.

Рис.1.32.

1.4.5. Рівняння руху та структурна схема двомасової розрахункової схеми механічної частини електропривода із зазором та урахуванням внутрішнього в’язкого тертя

Розрахункова схема представлена на рис.1.33. В даному випадку пружний момент М₁₂ та момент внутрішнього в’язкого тертя М_ВТ характеризуються нелінійною залежністю. Сумарний пружно-в’язкий момент визначається наступною формулою

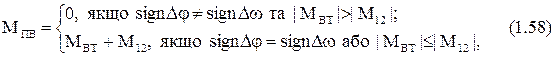
де М₁₂ = с₁₂ F₁(j) – пружний момент;

M_ВТ = b₁₂ Dw F₂(j) – момент в’язкого тертя;

F₁ та F₂ – нелінійні функції;

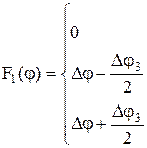
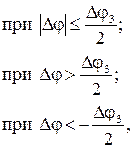
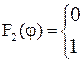
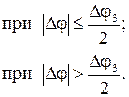
Система рівнянь, яка описує рух даної механічної частини, аналогічна (1.56), але до неї замість останнього рівняння підставляється (1.58).

Рис.1.33.

Відповідна структурна схема показана на рис.1.34.

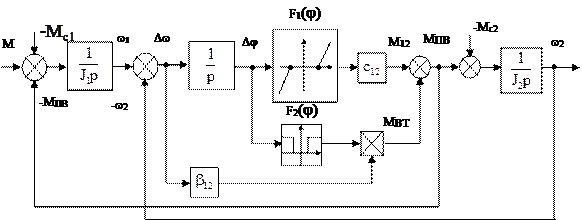Рис.1.34.

1.4.6. Рівняння руху механізмів із нелінійним кінематичним зв’язком

Ряд механізмів мають нелінійні кінематичні зв’язки, в яких радіус приведення параметрів залежить від кута повороту валу

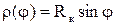, (1.59)

наприклад, кривошипно-шатунний механізм, рис.1.35. Узагальненою координатою є кут повороту вала j . Узагальнена сила дорівнює

Q` = M – M_с – F_сr(j) = M - M_cå(j), (1.60)

де M_cå(j) = M_с + F­_cR_кsinj – сумарний статичний момент.

Рис.1.35.

Кінетична енергія системи визначається наступним виразом

. (1.61)

На основі (1.60) та (1.61) складається рівняння Лагранжа, яке описує рух кривошипно-шатунного механізму

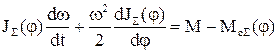. (1.62)

Рівняння руху (1.62) містить момент інерції J_å та статичний момент М_сå, які залежать від кута повороту валу, тобто періодично змінюються. Це ускладнює аналіз та синтез системи керування електроприводом.

1.5. Динамічні властивості пружної механічної частини електропривода

Аналіз властивостей пружної механічної частини електропривода проводиться на найбільш розповсюдженій двомасовій розрахунковій схемі без врахування внутрішнього в’язкого тертя. Аналіз здійснюється за керуючою змінною, якою є момент двигуна М. При цьому збурення, тобто статичний момент не враховується М_с1=М_с2=0. Після таких спрощень відповідна структурна схема, яка представлена на рис.1.25, приймає вигляд, рис.1.36.

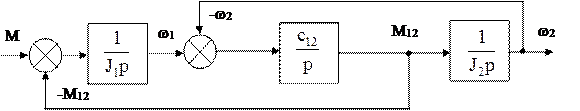Рис.1.36.

Для проведення аналізу здійснюється структурне перетворення. Для цього вузол із пружним моментом М₁₂ переноситься на вихід схеми, рис.1.37.

Рис.1.37.

На основі цієї структурної схеми визначається передаточна функція, яка зв’язує вихідну координату – швидкість другої маси ω₂ із швидкістю першої маси ω₁

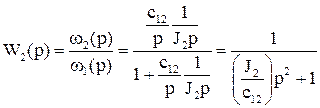. (1.63)

Передаточна функція W₂(p) являє собою ідеальну коливальну ланку.

Для визначення передаточної функції, яка зв’язує швидкість першої маси ω₁ з керуючою змінною – моментом двигуна М, структурна схема (1.37) представляється у наступному вигляді, рис.(1.38).

Рис.1.38.

Відповідна передаточна функція дорівнює

, (1.64)

де J_∑=J₁+J₂ – сумарний момент інерції системи.

Передаточна функція W₁(p) представляє собою послідовне з’єднання інтегруючої ланки, ідеальної коливальної ланки та ідеальної форсуючої ланки другого порядку.

Загальна передаточна функція пружної механічної частини, яка визначає результуючий зв’язок між ω₂(р) і М(р), дорівнює добутку отриманих функцій

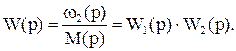(1.65)

Таким чином, початкова структурна схема двомасової розрахункової механічної частини електропривода представляється наступним чином, рис.1.39, рис.1.40.

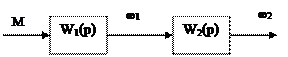
Рис.1.39.

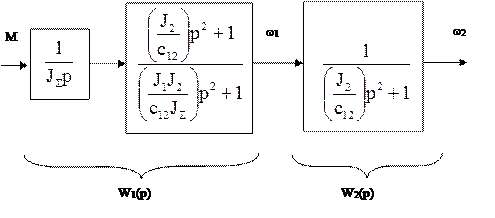Рис.1.40.

Після скорочення однакових чисельника W₁(p) та знаменника W₂(p) структурна схема приймає вигляд, рис.1.41.

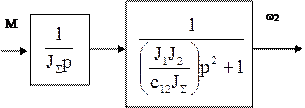Рис.1.41.

На основі структурної схеми, показаної на рис.1.41, записується характеристичне рівняння системи

, (1.66)

яке має три корені, із них один нульовий p₁=0 та два уявні

,

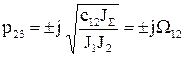де 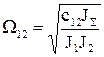- резонансна частота системи; (1.67)

Для зручності аналізу вводяться наступні параметри:

- співвідношення мас; (1.68)

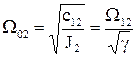- резонансна частота другої маси. (1.69)

Після цього передаточні функції (1.63), (1.64) можна записати у наступному вигляді

, (1.70)

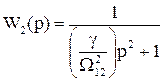. (1.71)

Так як функція W₁(p) (1.70) вміщує інтегруючу ланку

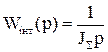(1.72)

з найбільшою сталою часу системи, що дорівнює сумарному моментові інерції J_S, то ця інтегруюча ланка й визначає характер руху в цілому. При незмінному значенні моменту двигуна М=const швидкість першої маси (двигуна) ω₁ змінюється за лінійним законом. Якщо частота коливання моменту двигуна наближається до частоти резонансу системи Ω₁₂, обумовлену ідеальною коливальною ланкою (знаменник функції W₁(p) )

,

то можливе суттєве збільшення амплітуди коливань. Але на цей процес впливають параметри форсуючої ланки (чисельник функції W₁(p) )

.

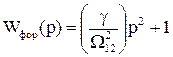Якщо момент інерції механізму незначний, тобто J₂<<J₁, то γ≈1 і форсуюча ланка компенсує дію коливальної. Крім того, якщо жорсткість зв’язку с₁₂ велика, то резонансна частота Ω₁₂ зміщується у високочастотну область за частоту зрізу системи і суттєво не впливає на рух, так як його характер визначається низькочастотною областю сформованою інтегруючою ланкою (1.72).

Функція W₂(p) (1.71) представляє собою коливальну ланку і при коливаннях моменту, близьких до резонансної частоти Ω₁₂ немає факторів, які б ослабили значні коливання другої маси (робочого органу).

Таким чином, якщо потрібно отримати задану якість керування робочим органом чи в системі керування використовуються зворотні зв’язки за координатами механізму, то обов’язково потрібно враховувати пружний зв’язок і при синтезі системи використовувати двомасову розрахункову схему. Якщо ж J₂<<J₁ чи жорсткість зв’язку достатньо висока і в системі керування не використовуються зворотні зв’язки за координатами другої маси, то механічну частину можна спростити до одномасової, не враховуючи пружність.

В реальних системах завжди присутні дисипативні сили внутрішнього в’язкого тертя, які демпфірують коливання, проте природне затухання незначне і суттєво не впливає на рух системи в цілому, хоча й зменшує величину резонансних піків.

Більш детальний аналіз динамічних властивостей пружної системи здійснюється за допомогою амплітудно-фазо-частотних характеристик.

1.6. Режими роботи електропривода

Основою для аналізу режимів роботи електропривода є отримані в підрозділі 1.4 диференційні рівняння руху одно-, дво- та тримасових розрахункових схем. В цілому рух механічної частини електропривода вірно описує одномасова схема, крім того, її найпростіше аналізувати. Цей рух описується основним рівнянням (1.38)

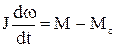. (1.73)

Права частина рівняння визначає характер керуючої та збурюючої дій. Керуючою дією для механічної частини ЕП є момент двигуна М, а збурюючою – статичний момент навантаження М_с, створюваний робочим органом механізму. Права частина називається також динамічним моментом

М_дин=М – М_с . (1.74)

Динамічний момент визначає прискорення двигуна та відповідно механізму

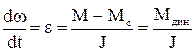. (1.75)

В залежності від значення динамічного моменту електропривод може знаходитися у статичному чи динамічному режимах.

Статичний режим має місце, якщо динамічний момент дорівнює нулю М_дин=0, тобто коли М=М_с. При цьому прискорення (1.75) також дорівнює нулю 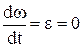і відбувається усталений рух із постійною швидкістю ω=const або електропривод не рухається ω=0. Механічні частини з нелінійними кінематичними зв’язками (кривошипно-шатунний, кулісний механізми тощо) не мають статичного режиму.

Динамічний режим наступає при М_дин≠0, тобто при M≠М_с, і наявності прискорення 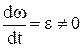. В залежності від знаків динамічного моменту та швидкості механічна частина може розганятися, якщо

М_дин>0; ; ω>0 чи М_дин<0; ;ω<0,

або сповільнюватися

М_дин>0; ; ω<0 чи М_дин<0; ;ω>0.

Динамічний режим обумовлює динамічний перехідний процес чи усталений динамічний процес. Перехідний процес представляє перехід від одного статичного режиму до іншого в часі, тобто перехід від однієї до іншої точок рівноваги. Усталений динамічний процес має місце, якщо в процесі руху механічної частини момент двигуна М чи статичний момент М_с змінюються в часі, наприклад, у кривошипно-шатунного механізму (1.29).

На рис.1.42 показано процес руху механічної частини. На ділянці І електропривод знаходиться у динамічному режимі, здійснюючи розгін механізму, тобто перехід від нульової до кінцевої швидкості ω_кін .

Рис.1.42.

При розгоні момент двигуна згідно (1.73) дорівнює

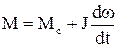(1.76)

й іде на подолання моменту опору механізму М_с та збільшення запасу кінетичної енергії системи, тобто на забезпечення заданого прискорення

. (1.77)

На ІІ ділянці електропривод працює у статичному режимі, рухаючись з усталеною швидкістю ω_кін . Момент двигуна витрачається тільки на подолання моменту опору М=М_с.

На ділянці ІІІ електропривод знову переходить у динамічний режим, сповільнюючи механізм до нульової швидкості. При цьому момент двигуна визначається величиною сповільнення

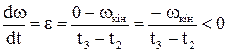(1.78)

та моментом опору і дорівнює

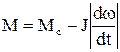. (1.79)

1.6.1. Статичні режими роботи електропривода

У статичному режимі момент двигуна врівноважується статичним моментом М=М_с та відсутнє прискорення =0. Для описання статичних властивостей двигунів та механізмів використовуються механічні характеристики ω=¦(М), тобто залежність швидкості від моменту. Механічні характеристики можуть мати вигляд кривих чи прямих ліній. На рис.1.43. представлено прямолінійні механічні характеристики двигуна постійного струму (ДПС), синхронного двигуна (СД) та механізму. Механічні характеристики характеризуються жорсткістю

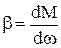. (1.80)

Рис.1.43.

Для прямолінійних характеристик жорсткість можна визначити за допомогою приростів моменту та швидкості

. (1.81)

Жорсткість механічної характеристики ДПС має від’ємне значення

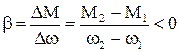, (1.82)

так як DM>0, а Dw<0 для точок А та В. Синхронний двигун СД має абсолютно жорстку механічну характеристику, тобто рівну нескінченності

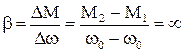, (1.83)

бо DM>0, а Dw=0. Механічна характеристика представленого механізму абсолютно м’яка, тобто рівна нулю

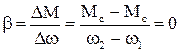, (1.84)

так як DM=0, а Dw<0. Якісно жорсткість механічних характеристик у порівнянні описується словами “жорстка”, “м’яка”, “жорсткіша”, “м’якіша”.

Механічна характеристика двигуна характеризується також швидкістю ідеального холостого ходу w₀ , пусковим моментом (моментом короткого замикання) М_п та номінальними швидкістю w_ні моментом М_н .

Двигун чи механізм може працювати в будь-якій точці на своїй механічній характеристиці. Конкретна робоча точка визначається перетином механічних характеристик двигуна та механізму. В робочій точці момент двигуна дорівнює статичному моментові, який створює механізм М=М_с. Двигун постійного струму ДПС працює в точці РТ1 із швидкістю w_с , а синхронний двигун СД – в точці РТ2 із швидкістю w₀.

Усталений рух у робочій точці може бути стійким чи нестійким. Умовою стійкого руху є

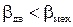, (1.85)

тобто жорсткість механічної характеристики двигуна β_дв повинна бути меншою жорсткості механічної характеристики механізму β_мех . Для ДПС ця умова виконується, бо в робочій точці РТ1

.

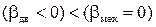Осі механічних характеристик на площині створюють чотири квадранти або четверті І-ІV, рис.1.44. Робоча точка двигуна в залежності від статичного моменту та режиму роботи може знаходиться в будь-якому квадранті. Якщо при цьому в робочій точці знаки швидкості та моменту співпадають, то двигун працює в рушійному режимі, передаючи енергію механізму, квадранти І, ІІІ.

Рис.1.44.

Якщо знаки швидкості та моменту різні, то двигун знаходиться в гальмівному режимі, отримуючи енергію від механізму, квадранти ІІ, ІV. Механічні характеристики двигуна для прямого та зворотного напрямку руху симетричні відносно початку координат, рис.1.44.

Двигун має природну механічну характеристику, яка відповідає його підключенню до мережі на номінальні (паспортні) дані. Крім того, двигун може мати будь-яку кількість штучних механічних характеристик, які відповідають підключенню на неномінальні дані. Штучні характеристики використовуються для зміни режиму роботи, швидкості, моменту двигуна тощо.

1.6.2. Механічні перехідні процеси

Перехідний процес, який обумовлений дією моменту двигуна чи статичного моменту називається механічним. (Є також електромеханічні перехідні процеси, які враховують ще й електромагнітні перехідні процеси в електричних обмотках двигуна та елементах силових перетворювачів. Електромеханічні перехідні процеси будуть розглядатися пізніше.) Основне рівняння руху (1.38) у цілому вірно описує механічні перехідні процеси

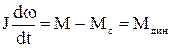. (1.86)

В залежності від закону зміни динамічного моменту механічні перехідні процеси розрізняються на процеси:

1) з постійним динамічним моментом М_дин=const;

2) з динамічним моментом, який лінійно залежить від швидкості М_дин=¦(ω);

3) з динамічним моментом, який довільно залежність від швидкості.

1.6.2.1. Перехідні процеси з постійним динамічним моментом

В даному випадку прискорення залишається незмінним

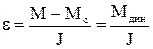. (1.87)

Вирішення рівняння (1.86) за умови незмінних значень М, М_с, J, e дозволяє отримати закон зміни швидкості при перехідному процесі

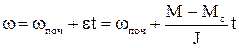. (1.88)

Згідно (1.88) швидкість лінійно залежить від часу. Якщо відомі початкове та кінцеве значення швидкості, то з (1.88) знаходиться час перехідного процесу

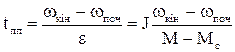. (1.89)

Закон зміни положення визначається з урахуванням (1.88) на основі рівняння для кута

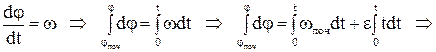
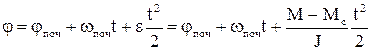. (1.90)

Відповідно до (1.90) кут залежить у квадраті від часу. Графіки перехідних процесів швидкості w=f(t) та кута j=f(t) при постійному динамічному моменті М_дин показано на рис.1.45.

Рис.1.45.

Типові випадки механічних перехідних процесів із постійним динамічним моментом наступні:

1) Пуск вхолосту до швидкості w_кін з різним прискоренням e₁> e₂ .

В даному випадку початкова швидкість w_поч=0,статичний момент відсутній М_с=0, тому динамічний момент (1.74) дорівнює моменту двигуна М_дин=М.

Рис.1.46.

Так як прискорення e₁> e₂ , то згідно (1.76) для їх забезпечення

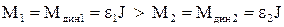, (1.91)

а час досягнення w_кін відповідно до (1.89)

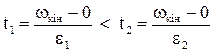. (1.92)

Після завершення перехідного процесу момент двигуна дорівнює нулю М=М_с=0. Графіки перехідних процесів швидкостей w₁=f(t), w₂=f(t), побудованих згідно (1.88), та моментів двигуна М₁=f(t), М₂=f(t) приведено на рис.1.46.

2) Зупинка від початкової швидкості w_поч з різним сповільненням |e₁|< |e₂| при відсутності статичного моменту.

В цьому випадку кінцева швидкість w_кін=0,статичний момент відсутній М_с=0, тому динамічний момент (1.74) дорівнює моменту двигуна М_дин=М. Так як сповільнення мають від’ємні значення і |e₁|< |e₂| , то згідно (1.79) для їх забезпечення моменти також повинні бути від’ємними, з наступними абсолютними значеннями

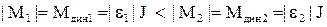, (1.93)

а час зупинки відповідно до (1.89)

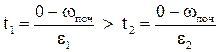. (1.94)

Після завершення перехідного процесу момент двигуна дорівнює нулю М=М_с=0. Графіки перехідних процесів швидкостей w₁=f(t), w₂=f(t), побудованих згідно (1.88), та моментів двигуна М₁=f(t), М₂=f(t) приведено на рис.1.47.

Рис.1.47.

3) Пуск при реактивному статичному моменті М_с до швидкості w_кін із заданим прискоренням e.

В даному випадку початкова швидкість w_поч=0,динамічний момент згідно (1.74) дорівнює М_дин=М-М_с. Для забезпечення заданого прискорення момент двигуна згідно (1.76) дорівнює

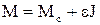, (1.95)

а час досягнення w_кін відповідно до (1.89)

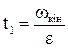. (1.96)

Після завершення перехідного процесу момент двигуна дорівнює статичному моменту М=М_с. Графіки перехідних процесів швидкості w=f(t), побудованого за (1.88), та моменту двигуна М=f(t) приведено на рис.1.48.

Рис.1.48.

4) Зупинка від початкової швидкості w_поч з різним сповільненням |e₁|< |e₂| при наявності статичного моменту М_с.

Кінцева швидкість w_кін=0.Момент двигуна до початку перехідного процесу врівноважується статичним моментом М=М_с. Динамічний момент під час перехідного процесу згідно (1.74) дорівнює М_дин=М-М_с. Так як сповільнення мають від’ємні значення і |e₁|< |e₂|, то згідно (1.79) моменти визначаються наступним чином

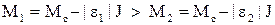. (1.97)

Як видно з (1.97) момент двигуна в залежності від величини сповільнення може змінювати знак чи дорівнювати нулю. В останньому випадку задане сповільнення буде забезпечуватися статичним моментом. Час зупинки відповідно до (1.89) дорівнює

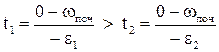. (1.98)

Після завершення перехідного процесу момент двигуна дорівнює статичному моментові М=М_с. При зупинці механізму двигун можна вимкнути, якщо статичний момент є реактивним, тобто не рушійним. Якщо ж статичний момент є активним, то відключення двигуна призведе до руху механізму під його дією. Графіки перехідних процесів швидкостей w₁=f(t), w₂=f(t), побудованих згідно (1.88), та моментів двигуна М₁=f(t), М₂=f(t) приведено на рис.1.49.

5) Реверс (зміна напрямку руху) від початкової швидкості w_поч до кінцевої швидкості w_кін при заданому моменті двигуна Мта при активному статичному моменті М_с.

Рис.1.49.

Момент двигуна до початку перехідного процесу врівноважується статичним моментом М=М_с. Останній не змінює свого знаку на протязі всього перехідного процесу, бо є активним. Для реалізації реверса напрямок моменту двигуна змінюється на протилежний, тому значення динамічного моменту на весь час перехідного процесу згідно (1.74) залишається незмінним М_дин=|М+М_с|. Цей динамічний момент забезпечує однакові значення сповільнення

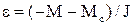(1.99)

та прискорення при розгоні у зворотному напрямку

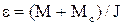. (1.100)

Рис.1.50.

Час перехідного процесу складається з проміжків сповільнення та розгону

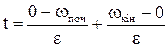. (1.101)

Після завершення перехідного процесу момент двигуна дорівнює статичному моментові М=М_с. Графіки перехідних процесів швидкості w=f(t), побудованого згідно (1.88), та моменту двигуна М=f(t) приведено на рис.1.50.

6) Реверс (зміна напрямку руху) від початкової швидкості w_поч до кінцевої швидкості w_кін при заданому моменті двигуна Мта при реактивному статичному моменті М_с.

Момент двигуна до початку перехідного процесу врівноважується статичним моментом М=М_с. Для реалізації реверса напрямок моменту двигуна змінюється на весь час перехідного процесу на протилежний. При зміні знаку швидкості статичний момент також змінює своє значення на протилежне, бо за своєю природою він є реактивним. Адже динамічний момент при сповільненні М_дин1=-М-М_с та при прискоренні М_дин2=-М+М_с має різне значення, тому значення сповільнення

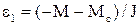(1.102)

більше за прискорення при розгоні у зворотному напрямку

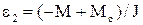, (1.103)

що обумовлює злам прямої на графіку перехідного процесу швидкості, рис.1.51.

Рис.1.51.

Час перехідного процесу складається з двох проміжків сповільнення та розгону

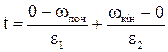. (1.104)

Після завершення перехідного процесу момент двигуна дорівнює статичному моментові М=М_с.

Якщо момент двигуна при зупинці буде меншим за статичний момент |М|<|М_с|, то двигун зупиниться і розгону механізму у зворотному напрямку не буде, рис.1.52.

Рис.1.52.

Перехідні процеси з постійним динамічним моментом часто використовуються для попередніх розрахунків поведінки механічної системи, бо потребують мінімум вихідних даних при вірному описі процесу в цілому. Реальні перехідні процеси з постійним динамічним моментом найчастіше формуються за допомогою замкненої системи керування електропривода.

1.6.2.2. Перехідні процеси з динамічним моментом, який лінійно залежить від швидкості

Багато двигунів та механізмів мають механічні характеристики з лінійним зв’язком між моментом та швидкістю, рис 1.53.

Рис.1.53.

Рівняння механічних характеристик двигуна та механізму згідно рис.1.53 мають вигляд

(1.105)

де b – жорсткість механічної характеристики двигуна;

b_с – жорсткість механічної характеристики механізму.

Сумісне вирішення рівнянь (1.105) з основним рівнянням динаміки (1.38)

дає рівняння руху одномасової розрахункової схеми

. (1.106)

Після по-членного ділення (1.106) на (b+b_с) отримується остаточне диференційне рівняння руху механічної частини

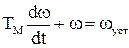, (1.107)

де 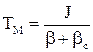- електромеханічна стала часу системи, [c];

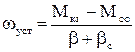- усталена швидкість, рис.1.53.

Якщо жорсткість механічної характеристики механізму b_с=0, то електромеханічна стала часу визначається жорсткістю механічної характеристики двигуна .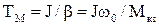

Розв`язок рівняння (1.107) визначається сумою загального і часткового рішень w=w_заг +w_част. Загальне рішення однорідного рівняння

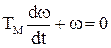(1.108)

знаходиться у вигляді

,

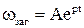де А – невідома константа;

р=-1/Т_м – корінь характеристичного рівняння T_мpw+w=0.

Остаточно загальне рішення приймає вид

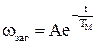. (1.109)

Часткове рішення знаходиться при нульовій похідній dw/dt=0 у рівнянні (1.107) і дорівнює

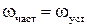. (1.110)

Таким чином, розв’язок рівняння (1.107) з урахуванням (1.109), (1.110) представляється у формі

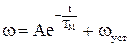. (1.111)

Константа Азнаходиться з (1.111) при початкових умовах часу t=0 та початкової швидкості w=w_поч

А=w_поч - w_уст,

після чого розв’язок остаточно матиме вигляд

. (1.112)

Рівняння (1.112) описує закон зміни швидкості під час перехідного процесу. Момент двигуна зв`язаний із швидкістю відомим рівнянням

,

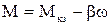і змінюється в часі аналогічно до швидкості

. (1.113)

Закон зміни положення (кута) знаходиться з рівняння

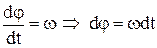
шляхом інтегрування після підстановки в його (1.112)

. (1.114)

Рівняння (1.112) та (1.113) дозволяють визначити час перехідного процесу від початкової швидкості w_поч чи початкового моменту М_поч до будь-якої точки w_i чи М_i перехідного процесу

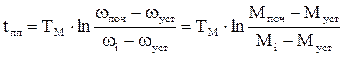. (1.115)

Як видно з (1.115), суттєвий вплив на тривалість перехідного процесу має електромеханічна стала часу Т_м. Фізична суть електромеханічної сталої часу – це час розгону двигуна при відсутності навантаження до швидкості ідеального холостого ходу w₀ під дією незмінного моменту рівного моменту короткого замикання М_кз. Значення електромеханічної сталої можна знайти з графіка перехідного процесу відомим методом дотичної. Теоретично перехідний процес завершується при t=¥. На практиці перехідний процес вважається завершеним, якщо перехідна координата досягла 0,95-0,98 від усталеного значення. При цьому час перехідного процесу дорівнює відповідно t_пп=(3¸4)Т_м. Графіки перехідних процесів швидкості w=f(t) та моменту двигуна М=f(t), побудованих згідно (1.112) та (1.113), приведено на рис.1.54.

Рис.1.54.

1.6.2.3. Перехідні процеси з динамічним моментом, який довільно залежить від швидкості

Нелінійна залежність динамічного моменту від швидкості характерна для асинхронних двигунів (АД), двигунів постійного струму з послідовним збудженням, а також струминних механізмів, рис.1.55.

Рис.1.55.

Вирішення відповідних диференційних рівнянь у цьому випадку для отримання залежностей, які описують перехідні процеси швидкості, моменту та положення, найчастіше здійснюється числовими методами Ейлера, Рунге-Кутта тощо за допомогою ЕОМ. У простих випадках можна використати графічне інтегрування чи спрощені аналітичні залежності.

1.6.2.4. Перехідний процес пуску електропривода, представленого двомасовою розрахунковою схемою

Перехідні процеси у двомасовій розрахунковій схемі для зменшення громіздкості та підвищення наочності розглядаються без врахування внутрішнього в'язкого тертя та механічного зазору при відсутності статичних моментів та при незмінному моменті двигуна М, рис.1.56.

Рис.1.56.

Дослідження здійснюється на основі раніше визначених у підрозділі 1.5. передаточних функцій

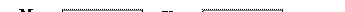
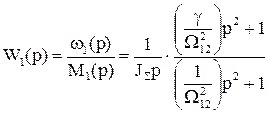; (1.116)

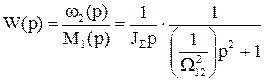. (1.117)

Після заміни в (1.116) отримується відповідне диференційне рівняння

,

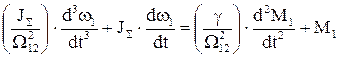яке при діленні на сумарний момент інерції J_S з урахуванням того, що похідна за моментом дорівнює нулю, бо М₁=const, приймає вигляд

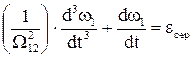, (1.118)

де - середнє прискорення системи.

Три корені рівняння знайдено раніше у підрозділі 1.5. Нульовий корінь р₁=0 визначає рівноприскорений рух системи із швидкістю 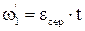, а два уявні корені р_2,3=±jW₁₂ – можливість незатухаючих коливань швидкості 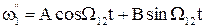на частоті W₁₂. Вирішення рівняння (1.118) знаходиться у наступному вигляді

. (1.119)

Невідомі коефіцієнти А і В визначаються з початкових умов t=0, w₁=0, dw₁/dt=M₁/J₁=ge_сер

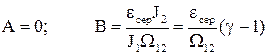
після чого закон зміни швидкості першої маси під час перехідного процесу приймає вигляд

. (1.120)

Аналогічно на основі передаточної функції (1.118) знаходиться закон зміни швидкості другої маси

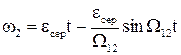. (1.121)

Як видно з (1.120) та (1.121) рух двомасової системи при постійному динамічному моменті проходить рівноприскорено, але обидві маси здійснюють коливання у протифазі, рис.1.57.

Рис.1.57.

Коефіцієнти при тригонометричних функціях e_сер(g-1)/W₁₂ та e_сер/W₁₂ визначають амплітуду цих коливань. При співвідношенні мас g=2 амплітуда коливань обох мас однакова. Амплітуда коливань тим менше, чим менше прискорення e_сер та чим більша частота коливань W₁₂, яка в свою чергу залежить від жорсткості зв’язку. На зменшення амплітуди коливань першої маси впливає зменшення моменту інерції другої маси.

В реальних системах завжди присутні дисипативні сили типу внутрішнього в’язкого тертя, які поглинають коливання. В такому випадку з трьох коренів характеристичного рівняння один є нульовим, а два інші - комплексно-спряжені

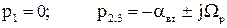
де 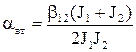- коефіцієнт демпфірування коливань;

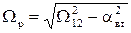- резонансна частота системи.

Механічна частина має властивості інтегруючої та коливальної ланок. Закони зміни швидкостей двох мас мають наступний вид

; (1.122)

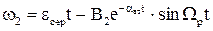. (1.123)

Проте природне затухання незначне, так логарифмічний декремент затухання дорівнює

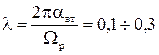
тобто коливання затухають за 10¸30 періодів, рис.1.58.

Рис.1.58.

1.7. Динамічні навантаження електропривода

Динамічні навантаження виникають у перехідних процесах: пуск, зупинка, зміна швидкості, зміна навантаження тощо. Вони викликають короткочасні перевантаження двигуна та елементів кінематичного ланцюга, тим самим зменшуючи надійність та довговічність ЕП та механізму. Якщо механічна частина представляється одномасовою схемою, то динамічне навантаження дорівнює динамічному моментові

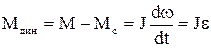. (1.124)

Найчастіше за технологічними вимогами задається середнє чи максимальне прискорення механізму e_max . В цьому випадку максимальний момент двигуна

не повинен перевершувати максимально допустимого значення, яке визначається паспортними даними чи 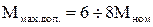для високомоментних двигунів. При прискоренні механізму динамічний момент (1.124) є гальмівним, а при сповільненні - рушійним.

Динамічні навантаження на елементи механічної частини суттєво збільшуються при виникненні пружних коливань та ударів при виборі зазорів. Пуск електропривода, механічна частина якого представляється двомасовою розрахунковою схемою із зазором (рис.1.30), найчастіше проходить в три етапи:

1) Вибір зазору, тобто рух тільки першої маси;

2) Зрушення другої маси;

3) Сумісний рух двох мас.

1) Вибір зазору.

Якщо зазор повністю розімкнено (найгірший випадок), то при реактивному статичному моменті М_с2 друга маса залишається нерухомою, а перша маса стрімко набирає швидкість під дією моменту двигуна (М_с1»0, М₁₂=0)

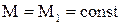
До удару з другою масою перша маса досягає швидкості

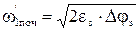
де 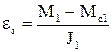- прискорення при виборі зазору.

2) Зрушення другої маси.

При ударі, тобто при замиканні зазору, друга маса залишається нерухомою поки пружний момент М₁₂ не стане більше статичного моменту М_с2, тому швидкість першої маси ще збільшується до w_1поч .

3) Сумісний рух двох мас.

Після зрушення другої маси динамічне навантаження визначається пружним моментом. З відомої системи рівнянь (1.53), яка описує двомасову схему знаходиться рівняння пружного моменту у вигляді

, (1.125)

де 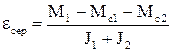- середнє прискорення механічної частини, якби пружний зв’язок був абсолютно жорстким.

Рішення даного рівняння знаходиться як сума загального та часткового при коренях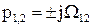

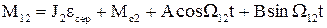. (1.126)

Коефіцієнти А та В знаходяться з початкових умов

,

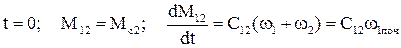після чого закон зміни пружного моменту дорівнює

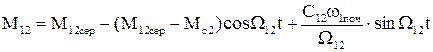, (1.127)

де 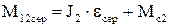- середній пружний момент;

або

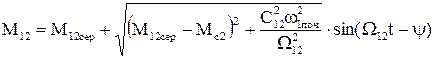, (1.128)

де 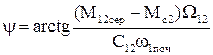- фаза.

Графіки перехідних процесів швидкостей та моменту представлено на рис.1.59.

Рис.1.59. t_з – час замикання зазору.

Динамічне навантаження характеризується динамічним коефіцієнтом, як відношення максимального пружного моменту (1.128) при sin(W₁₂t-y)=1 до середнього

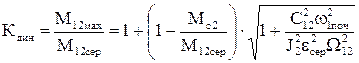. (1.129)

Згідно (1.129), якщо зазор до початку пуску було замкнено і w_1поч=0 та М_с2=0, то К_дин=2, тобто пружний момент вдвічі збільшує навантаження. Якщо ж зазор розімкнено w_1поч¹0, то перевантаження буде тим більше, чим більший момент інерції першої маси J₁ та жорсткість с₁₂. Таким чином, пружність зв’язку зменшує динамічні удари. При проектуванні ЕП та механізму потрібно забезпечити динамічний коефіцієнт, близький до К_дин=1, що дозволить збільшити надійність та довговічність механізму. В цілому динамічні коливання мас не впливають на тривалість перехідного процесу, але негативно позначаються на виконанні технологічних операцій, особливо на точності роботи.

1.8. Оптимізація передаточного числа кінематичного ланцюга (редуктора)

Безпосереднє з’єднання двигуна з робочим органом є найбільш надійним, проте не завжди можливим, бо двигуни випускаються на певні ряди швидкостей, а, крім того, більшість робочих органів рухається з невеликою швидкістю й виготовлення двигунів на такі швидкості неекономічне. Тому виникає задача про раціональне значення коефіцієнта передачі кінематичного ланцюга (редуктора) - i. Критерії оптимізації можуть бути різними. Для багатьох механізмів та слідкуючих систем потрібно забезпечити максимальне прискорення у перехідних процесах. Рівняння руху, записане відносно швидкості робочого органу w_ро, має вигляд

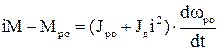, (1.130)

де М, М_ро- момент двигуна та статичний момент робочого органу;

J_д, J_ро- моменти інерції двигуна та робочого органу.

Прискорення згідно (1.130) дорівнює

. (1.131)

Оптимальне значення коефіцієнта передачі редуктора, яке забезпечує максимальне прискорення, знаходиться відомим способом із рівняння похідної

.

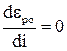Після перетворень оптимальне значення передаточного числа дорівнює

. (1.132)

Вираз (1.132) вірний і для найбільшого сповільнення системи. Задача одночасного забезпечення максимальних прискорення та сповільнення однозначно вирішується тільки при відсутності статичного моменту, тобто при підстановці у (1.132) значення М_ро =0.