Класичній механіці

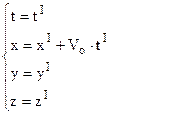
Розглянемо інерціальну систему К(x,y,z) і систему К¹(x¹,y¹,z¹), яка рухається відносно системи К з постійною швидкістю вздовж осі х. Для простоти будемо вважати, що осі y і z паралельні осям y¹ і z¹ відповідно. Нехай начала координат 0 і 0¹ в початковий момент часу співпадають (рис.3.4). Тоді запишемо очевидні із рис.3.4 співвідношення між координатами в якийсь момент часу t = t¹: 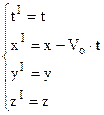. (3.4)

Рівняння (3.4) називаються перетвореннями координат Галілея, які справедливі для швидкостей набагато менших від швидкості світла.

Розглянемо наслідки цих перетворень.

a) Візьмемо перші похідні за часом

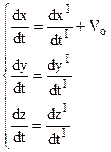
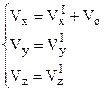, або (3.5)

Одержали правило складання швидкостей в класичній механіці: абсолютна швидкість 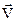дорівнює векторній сумі відносної і переносної швидкостей.

Наприклад, човен пливе по річці. Швидкість течії ріки – це переносна швидкість, відносна – це швидкість човна відносно води, тобто в стоячій воді, абсолютна – це результуюча швидкість човна відносно берега.

б) Візьмемо ще раз з рівняння (3.5) похідні за часом

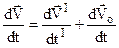. Так як 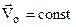, , 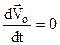або .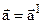

У всіх інерціальних системах прискорення однакове, або кажуть, що другий закон Ньютона інваріантний (незмінний) в усіх інерціальних системах відліку.

Принцип відносності Галілея: У всіх інерціальних системах відліку одні і ті ж механічні явища протікають однаковим чином і ніякими механічними дослідами, які проводяться всередині інерціальної системи, неможливо встановити – рухається вона чи ні.