Определение коэффициентов канонических уравнений. Коэффициенты канонических уравнений метода перемещений можно определять статическим или кинематическим способами.

Коэффициенты канонических уравнений метода перемещений можно определять статическим или кинематическим способами.

Статический способ основан на определении реакций во введенных связях основной системы из уравнений статики. Для этого необходимо вырезать отдельные узлы или части основной системы и составлять уравнения равновесия (статики). Если искомая реакция является реактивным моментом, то она определяется из условия равенства нулю момента в узле SM=0, если же она является реактивной силой, то определяется из уравнения проекции на ось (например, на ось x) в направлении этой реакции SX=0. Статический способ достаточно прост для использования, поэтому является основным способом определения коэффициентов системы канонических уравнений.

Докажем одну полезную теорему.

Теорема Релея. Реакция, возникающая в j-ой связи от перемещения i-ой связи на единицу, равна реакции i-ой связи от перемещения j-ой связи на единицу, т.е. .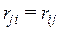

Доказательство. Рассмотрим i-ое и j-ое единичные состояния основной системы некоторой рамы (рис. 11.3 а, б) и соответствующие эпюры моментов в этих состояниях (рис. 11.3 г, д).

Возможная работа сил j-ого единичного состояния (рис. 11.3 б) на перемещениях i-го состояния (рис. 11.3 а) равна

.

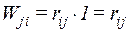Работа сил i-го состояния на перемещениях j-го состояния будет

.

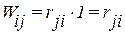По теореме Бетти 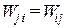. Значит, равны и правые части, т.е. .

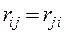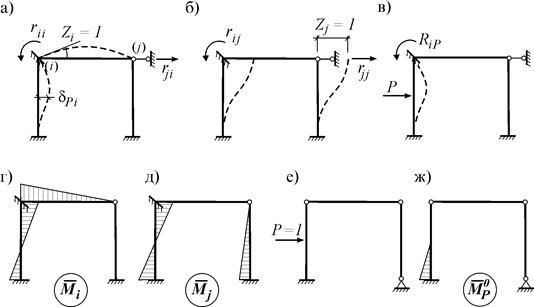
Рис. 11.3

Эту теорему иногда называют теоремой о взаимности реакций. Она позволяет сократить объем вычислений побочных коэффициентов канонических уравнений.

Кинематический способ основан на определении коэффициентов канонических уравнений перемножением эпюр. Этот способ применяется при сложности определения коэффициентов статическим способом или для проверки результатов статического способа.

Для вывода формулы кинематического способа определим две возможные работы. Работа внешних сил j-го единичного состояния на перемещениях i-го состояния нам известна: 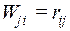. А возможная работа внутренних сил j-го единичного состояния на деформации i-го состояния 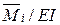равна:

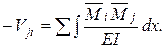
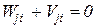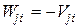По принципу возможных перемещений или . Отсюда получаем искомую формулу:

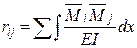или .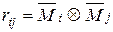

Формула вычисления грузовых коэффициентов отличается от аналогичной формулы метода сил (дается без вывода):

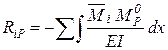или ,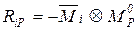

где 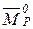– грузовая эпюра изгибающих моментов в любой статически определимой системе, полученной из заданной системы удалением лишних связей.