Дискретная модель стержневой системы
 |  |
Выбор дискретной расчетной модели стержневой системы начинается с разбиения расчетной схемы на элементы – на стержни постоянного сечения. В плоской стержневой системе эти элементы могут соединяться в шарнирном или жестком узлах (рис. 12.1):
шарнирный узел жесткий узел
Рис. 12.1
Здесь u1, u2, u3 – независимые перемещения узла (u1, u2 – линейные перемещения, u3 – угловое перемещение). У шарнирного узла число независимых перемещений равно двум, а у жесткого – трем. Они называются степенями свободы узла.
Общее число степеней свободы дискретной модели определяется суммой чисел степеней свободы отдельных узлов. Если обозначить его через n, а все перемещения узлов пронумеровать рядом натуральных чисел от 1 до n и объединить в единый вектор, получим
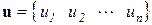 .
.
Он называется вектором перемещений дискретной модели.
Если в расчетной схеме имеются стержни переменного сечения, их следует представить в виде нескольких стержней постоянного сечения, а в места скачков сечений необходимо вводить узлы. В системах с криволинейными стержнями (в арках, кольцах и др.) криволинейные элементы следует заменять ломаной фигурой – многоугольником.
В дискретном методе нагрузка может быть приложена только в узлах. Однако в расчетной схеме нагрузка может быть и распределенной, и приложенной в виде сосредоточенных сил в точках, не совпадающих с узлами. Такие нагрузки следует переносить в соседние узлы как узловые силы, действующие в направлении степеней свободы дискретной модели. В результате этого формируется вектор внешней нагрузки
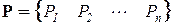 .
.
Внутренние усилия и деформации, которые требуется определить, также собираются в отдельные вектора
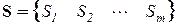 ,
,
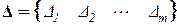 ,
,
где S – вектор усилий, Δ – вектор деформаций, m – число усилий.
Внешнюю нагрузку в узлы можно переносить по-разному.
В качестве примера рассмотрим три варианта переноса распределенной нагрузки q, действующей на балку (рис. 12.2 а), в узел расчетной модели, введенной в середине этой балки (рис. 12.2 б).
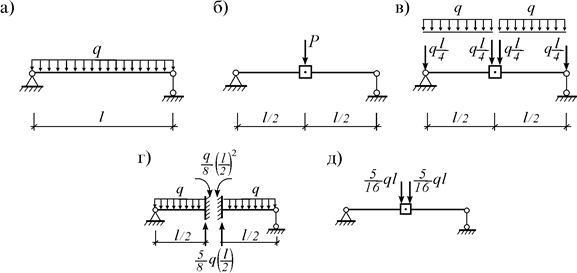
Рис. 12.2
Дата добавления: 2015-06-17; просмотров: 1371;
