Определение коэффициентов канонических уравнений

Коэффициенты при неизвестных 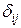и грузовые коэффициенты D_iP системы канонических уравнений – возможные перемещения от единичных сил и нагрузки. У них есть два индекса. Первый индекс i указывает на направление, а второй индекс j (или P) – на причину перемещения.

Методику вычисления этих коэффициентов рассмотрим на примере условной статически неопределимой системы (рис. 7.4 а) и ее основной системы (рис. 7.4 б).

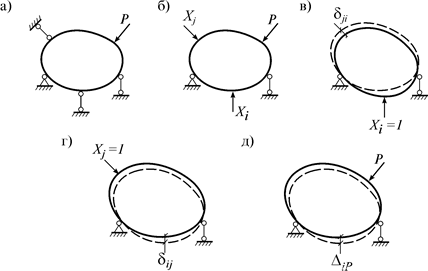
Рис. 7.4

Для определения коэффициентов 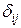рассмотрим два состояния ОС:

1) i-ое единичное состояние – воздействие силы X_i=1 (рис. 7.4 в);

2) j-ое единичное состояние – воздействие силы X_j=1 (рис. 7.4 г).

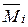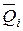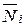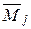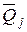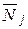Если в этих состояниях возникают внутренние усилия , , и , , , то возможная работа внутренних сил i-го состояния на деформациях j-го состояния будет:

–V_ij= 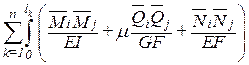dx.

С другой стороны, возможная работа внешних сил i-го состояния на перемещениях j-го состояния равна

W_ij=1×d_ij=d_ij .

По принципу возможных перемещений W_ij=–V_ij. Приравнивая их получаем формулу для вычисления коэффициентов при неизвестных:

d_ij= 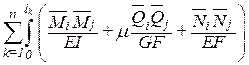dx .

Теорема Максвелла. Перемещение в i-ом направлении от единичной силы в j-ом направлении равна перемещению в j-ом направлении от единичной силы в i-ом направлении, т.е. d_ij=d_ji .

Доказательство. Возможную работу сил i-го единичного состояния (рис. 7.4 в) на перемещениях j-го состояния (рис. 7.4 г) мы уже знаем: W_ij=d_ij. А возможная работа сил j-го состояния на перемещениях i-го состояния равна W_ji=1×d_ji=d_ji. По теореме Бетти W_ij=W_ji. Следовательно, d_ij=d_ji .

Эта теорема позволяет уменьшать объем вычислений при нахождении боковых коэффициентов системы канонических уравнений.

Теперь выведем формулу вычисления грузовых коэффициентов.

Вначале определим возможную работу сил i-го единичного состояния (рис. 7.4 в) на перемещениях грузового состояния (рис. 7.4 д):

W_iP=1×D_iP=D_iP .

С другой стороны, возможная работа внутренних сил 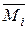, , 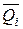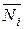i-го единичного состояния на деформациях грузового состояния равна

–V_iP= 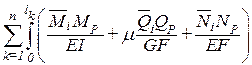dx.

По принципу возможных перемещений W_iP= –V_iP. Приравнивая их получим формулу вычисления грузовых коэффициентов: D_iP= 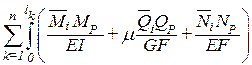dx.

Так как в рамах и балках перемещения определяются в основном изгибными деформациями, то коэффициенты канонических уравнений можно вычислять по сокращенным формулам:

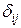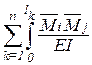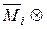
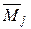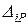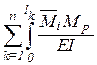= dx= ,

= dx= ,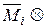

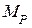где знак 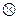используется для сокращения записи формулы вычисления интеграла Мора и означает условное «произведение» двух эпюр.