Понятие о статически неопределимых системах

Статически неопределимой называется система, внутренние усилия которой нельзя определить только из уравнений статики (равновесия). Статически неопределимые системы (СНС) отличаются от статически определимых рядом свойств:

1. Они надежнее, разрушение некоторых элементов не всегда приводит к разрушению всей системы.

2. Они выдерживают бо́льшую нагрузку.

3. У них деформации меньше.

4. Изменение температуры, смещение опор, неточность изготовления элементов вызывают дополнительные усилия.

5. Внутренние усилия зависят от физических и геометрических характеристик элементов.

У статически неопределимых систем есть так называемые «лишние» связи, число которых называется степенью статической неопределимости. Степень статической неопределимости n простой системы определяется из дискового аналога по следующей формуле:

.

Например, степени статической неопределимости балки (рис. 7.1 а) и рамы (рис. 7.1 в) будут:

n=2·0+0+4–3·1=1 и n=2·0+1+4–3·1=2.

Использование этой формулы при расчете сложных рам затруднительно. Поэтому можно применить другой подход, вводя два понятия: 1) замкнутый контур – замкнутая цепь из элементов и связей системы; 2) удалённая связь – связь замкнутого контура, исключенная из жесткого соединения элементов (см. рис. 7.1 б, г, е).

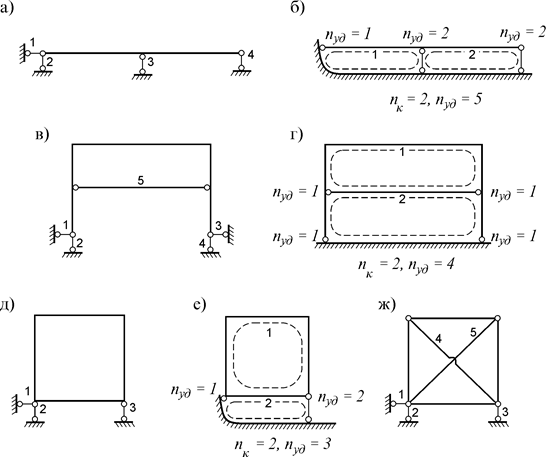
Рис. 7.1

Степень статической неопределимости сплошного замкнутого контура равняется трем. Поэтому степень статической неопределимости системы из n_к замкнутых контуров, из которых удалены n_уд связей, будет

n=3n_к – n_уд.

При использовании этой формулы для балки (рис. 7.1 а) и рам (рис. 7.1 в, д) в этих системах необходимо определить общее число замкнутых контуров n_к и удаленных связей n_уд (рис. 7.4 б, г, е). Тогда

− для балки: n=3×2–5=1;

− для рам: n=3×2–4=2, n=3×2–4=2.

Степень статической неопределимости фермы определяется по формуле

n= n_С+ n –2n_У .

Например, для фермы (рис. 7.1 ж): n=6+3–2×4=1.