Интеграл Мора. Определение перемещений
Рассмотрим два состояния стержневой системы:
1) грузовое состояние (рис. 6.6 а), в котором действующая нагрузка вызывает внутренние усилия MP, QP, NP;
2) единичное состояние (рис. 6.6 б), в котором действующая единичная сила P=1 вызывает внутренние усилия 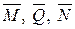 .
.
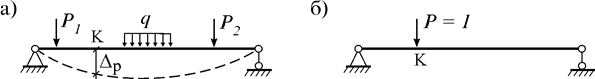
Рис. 6.6
Внутренние силы грузового состояния на деформациях единичного состояния 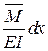 ,
, 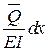 ,
, 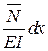 совершают возможную работу
совершают возможную работу
–Vij= 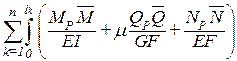 dx.
dx.
А единичная сила P=1 единичного состояния на перемещении грузового состояния DP совершает возможную работу
Wij=1×DP=DP .
По известному из теоретической механики принципу возможных перемещений в упругих системах эти работы должны быть равными, т.е. Wij= –Vij. Значит, должны быть равны и правые части этих выражений:
DP= 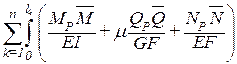 dx .
dx .
Эта формула называется формулой Мора и используется для определения перемещений стержневой системы от внешней нагрузки.
Рассмотрим отдельные случаи применения формулы Мора.
1. В балках (рис. 6.7 а) возможны три случая:
− если 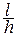 > 8, в формуле оставляется только член с моментами:
> 8, в формуле оставляется только член с моментами:
DP= 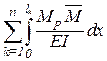 ;
;
− если 5≤ 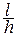 ≤8, учитываются и поперечные силы:
≤8, учитываются и поперечные силы:
DP=  dx;
dx;
− если 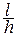 < 5, формула Мора дает большие погрешности. В этом случае перемещения следует определять методами теории упругости.
< 5, формула Мора дает большие погрешности. В этом случае перемещения следует определять методами теории упругости.
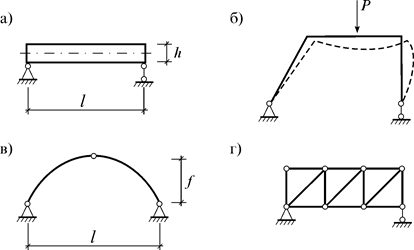
Рис. 6.7
2. В рамах (рис. 6.7 б) элементы в основном работают только на изгиб. Поэтому в формуле Мора учитываются только моменты.
В высоких рамах учитывается и продольная сила:
DP= 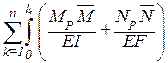 dx .
dx .
3. В арках (рис. 6.7 в) необходимо учитывать соотношение между основными размерами арки l и f:
1) если 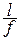 £ 5 (крутая арка), учитываются только моменты;
£ 5 (крутая арка), учитываются только моменты;
2) если 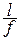 >5 (пологая арка), учитываются моменты и продольные силы.
>5 (пологая арка), учитываются моменты и продольные силы.
4. В фермах (рис. 6.7 г) возникают только продольные силы. Поэтому
DP = 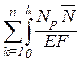 dx=
dx= 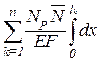 =
= 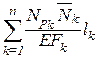 .
.
Дата добавления: 2015-06-17; просмотров: 1263;
