Возможные работы внешних и внутренних сил

Малое перемещение, допускаемое связями системы, называется возможным перемещением. Причиной возможного перемещения могут быть другие силы, изменение температуры, осадки опор и др.

Работа силы на ее возможном перемещении называется возможной работой. Возможное перемещение обозначим D_ij, а возможную работу W_ij (здесь i означает направление, а j – причину).

Например, если в некоторой точке балки действует сила P_i, а затем в другой точке начнет действовать другая сила P_j, то балка в точке действия силы P_i получит возможное перемещение D_ij (рис. 6.4 а). Так как в это время сила P_i остается постоянной, совершаемая ею возможная работа определяется площадью прямоугольника (рис. 6.4 б):

W_ij=P_iD_ij .

Таким образом, возможная работа равна произведению силы на возможное перемещение.

Рис. 6.4

При определении возможной работы следует рассматривать два состояния системы: в одном из них действуют заданные, а во втором – возможные силы.

Теорема Бетти. Возможная работа сил i-го состояния на перемещениях j-го состояния равна возможной работе сил j-го состояния на перемещениях i-го состояния.

Доказательство. Пусть на систему воздействуют силы P_i и P_j. Приложим их в разной последовательности и рассмотрим два состояния системы:

1) прикладывается сила P_i, затем сила P_j (рис. 6.5 а);

2) прикладывается сила P_j, затем сила P_i (рис. 6.5 б).

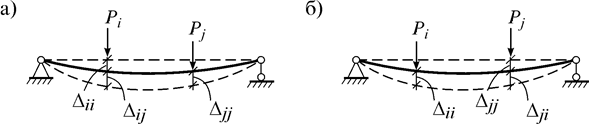
Рис. 6.5

В этих состояниях силы на действительных перемещениях совершают действительные, а на возможных перемещениях – возможные работы. Выражения работ в обоих состояниях будут:

W_ij= 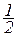P_iD_ii+ 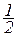P_jD_jj+P_iD_ij; W_ji= 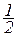P_jD_jj+ 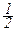P_iD_ii+P_jD_ji.

На основании принципа суперпозиции результат воздействия этих сил не зависит от порядка их приложения. Следовательно, обе работы равны: W_ij=W_ji. Отсюда получаем

P_iD_ij=P_jD_ji .

Теорема доказана. Ее часто называют теоремой о взаимности работ.

Теперь определим возможную работу внутренних сил. Для этого рассмотрим два состояния системы:

1) действует сила P_i и вызывает внутренние усилия M_i, Q_i, N_i;

2) действует сила P_j, которая в пределах малого элемента dx вызывает возможные деформации

D_Mj= 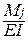dx, D_Qj=m 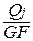dx, D_Nj= 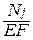dx.

Внутренние усилия первого состояния на деформациях (возможных перемещениях) второго состояния совершат возможную работу

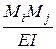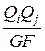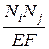–dV_ij=M_iD_Mj+Q_iD_Qj+N_iD_Nj= dx+m dx+ dx .

Если проинтегрировать это выражение по длине элемента l и учесть наличие в системе n стержней, получим формулу возможной работы внутренних сил:

–V_ij= 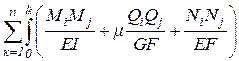dx .