II. Методика работы. Интерференция – это особый случай суперпозиции волн

Интерференция – это особый случай суперпозиции волн. При интерференции встречающиеся волны в одних точках пространства усиливают друг друга, в других – ослабляют, в зависимости от разности фаз (разности хода). Интерферировать могут лишь когерентные волны (или волны, идущие от когерентных источников). Когерентными являются волны одинаковой частоты, которые в любую точку пространства проходят с постоянной во времени разностью фаз.

Важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс называется стоячей волной. Практически стоячие волны возникают при отражении волн от преград. Стоячие волны могут возникать, например, в воздушном столбе при отражении волны от стенки, или в металлическом стержне при отражении волны от воздушной среды. В первом случае происходит потеря полуволны при отражении. Действительно, приходящая волна не в состоянии раскачать частицы стенки, и для них смещение от положения равновесия равно нулю.

Падающая на преграду волна и бегущая ей навстречу отраженная волна, налагаясь друг на друга, дают стоячую волну.

Так, если уравнение прямой бегущей волны

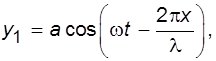(5.1)

то для отраженной волны оно запишется так

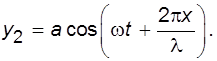(5.2)

В результате их сложения возникает волна, уравнение которой будет иметь следующий вид:

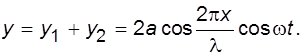(5.3)

Из выражения (5.3) видно, что в каждой точке стоячей волны происходят колебания той же частоты, что и у встречных волн, причем особенностью стоячей волны является зависимость амплитуды колебаний

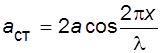(5.4)

от координаты (х). В тех точках, где разность фаз между падающей и отраженной от границы раздела волнами равна 0 или кратна 2p, колебания частиц среды происходят с удвоенной амплитудой (2а). Эти точки называются пучностями волны. Из уравнения (5.4) рассчитывают значения координат пучностей:

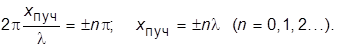(5.5)

В точках, где разность фаз равна p или нечетному числу p (падающая и отраженная волны встречаются в противоположных фазах), амплитуда колебаний уменьшается до нуля – происходит «гашение» колебаний. Эти точки называются узлами волны. Координаты узлов имеют значения

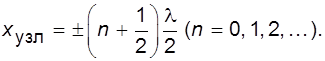(5.6)

Поскольку пространственное расположение узлов и пучностей не меняется со временем, то такая волна названа стоячей. Расстояние между соседними узлами (или пучностями) равно половине длины волны. Этими свойствами стоячих волн пользуются в лабораторных работах по определению скорости звука.

При этом на концах стержня будут пучности, а в центре его узел и поэтому длина волны распространяющихся в стержне колебаний равна

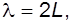(5.7)

где L – длина стержня.

Частота основного тона колебаний в стержне – n равна

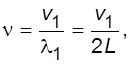(5.8)

где V₁ – скорость звука в стержне.

Колеблющийся стержень возбуждает в воздушном столбе стеклянной трубки звуковую волну, распространяющуюся в направлении стенки, с той же частотой от источника – основного тона колебаний в стержне. Следовательно, при этом будет иметь место соотношение

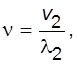(5.9)

где V₂– скорость звука в воздухе, l₂ – длина волны в воздухе.

Из (5.8) и (5.9) следует

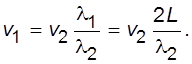(5.10)

С учетом температурной поправки скорость распространения звука в воздухе определяется по формуле

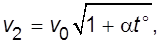(5.11)

где V₀ = 331 м/сек – скорость распространения звука в воздухе при нормальных условиях;

a = 0,004 – коэффициент расширения влажного воздуха;

t° – температура воздуха по Цельсию.

Для определения величины l₂ в стеклянную трубку насыпают немного опилок, которые при распространении колебаний в воздушном столбе трубки примут вид характерных фигур Кундта (рис. 5.2). Очевидно, что пучности в трубке соответствуют максимумам разброса опилок в трубке.

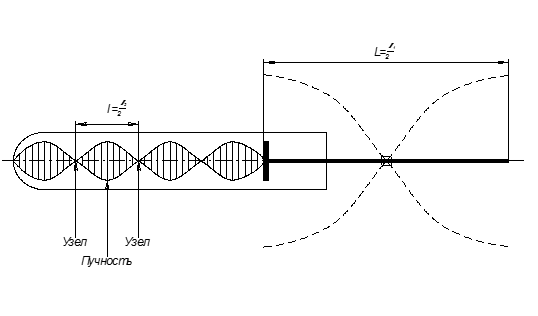
Рис.5.2. Расположение узлов и пучностей в стоячей волне

Фигуры Кундта образуются особенно ясно, когда расстояние от диска 3 дозакрытого конца трубки равно целому числу полуволн l/2; этого добиваются в опыте смещением трубки в ту или иную сторону относительно диска.

Очевидно, что 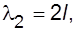(5.7а)

где l – длина фигуры Кундта.

Решая совместно (5.8), (5.9) и (5.11), получим расчетную формулу для определения скорости распространения звука в стержне

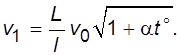(5.12)