Число степеней свободы молекулы. Закон равномерного распределения энергии по степеням свободы молекул

Важной характеристикой термодинамической системы является ее внутренняя энергия U– энергия теплового движения микрочастиц системы (молекул, атомов, электронов, ядер и т. д.) и энергия взаимодействия этих частиц.

Внутренняя энергия – однозначная функция термодинамического состояния системы, т.е. в каждом состоянии система обладает вполне определенной внутренней энергией (она не зависит от того, как система пришла в данное состояние). Это означает, что при переходе системы из одного состояния в другое изменение внутренней энергии определяется только разностью значений внутренней энергии этих состояний и не зависит от пути перехода.

Введем понятие числа степеней свободы i: это число независимых переменных (координат), полностью определяющих положение системы в пространстве. В ряде задач молекулу одноатомного газа рассматривают как материальную точку, которой приписывают три степени свободы поступательного движения (i=3). При этом энергию вращательного движения можно не учитывать.

В классической механике молекула двухатомного газа в первом приближении рассматривается как совокупность двух материальных точек, жестко связанных недеформируемой связью. Эта система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения. Вращение вокруг третьей оси (оси, проходящей через оба атома) лишено смысла. Таким образом, двухатомный газ обладает пятью степенями свободы (i=5). Трехатомнаяи многоатомная нелинейные молекулы имеют шесть степеней свободы: три поступательных и три вращательных (i=6).

Естественно, что жесткой связи между атомами не существует. Поэтому для реальных молекул необходимо учитывать также степени свободы колебательного движения.

На каждую степень поступательного движения приходится в среднем одинаковая энергия, равная 1/3 значения <w₀>:

<w₀>= 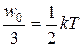. (7.1)

Колебательная степень «обладает» вдвое большей энергией потому, что на нее приходится не только кинетическая энергия (как в случае поступательного и вращательного движений), но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы. Таким образом, средняя энергия молекулы

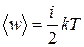, (7.2)

где i – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы.

Так как в идеальном газе взаимная потенциальная энергия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия, отнесенная к одному молю газа, будет равна сумме кинетических энергий N_А молекул:

U_m 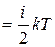N_А. (7.3)

Внутренняя энергия для произвольной массы т газа

U 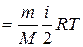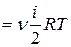, (7.4)

где Μ – молярная масса газа, ν – количество вещества.