Закон Максвелла о распределении молекул идеального газа по скоростям
При выводе основного уравнения молекулярно-кинетической теории молекулам задавали различные скорости. В результате многократных соударений скорость каждой молекулы изменяется по модулю и направлению. Однако из-за хаотического движения молекул все направления движения являются равновероятными, т.е. в любом направлении в среднем движется одинаковое число молекул.
По молекулярно-кинетической теории, как бы ни изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул массой m0 в газе, находящемся в состоянии равновесия при Т= const, остается постоянной и равной υcк=  . Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически вывел английский физик Дж. Максвелл. При выводе закона распределения молекул по скоростям Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют.
. Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически вывел английский физик Дж. Максвелл. При выводе закона распределения молекул по скоростям Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют.
Закон Максвелла описывается некоторой функцией f(υ), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скоростей будет приходиться некоторое число молекул dΝ(v), имеющих скорость, заключенную в этом интервале. Функция f(v) определяет относительное число молекул 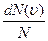 , скорости которых лежат в интервале от v до υ+dυ, т.е.
, скорости которых лежат в интервале от v до υ+dυ, т.е. 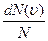 =f(υ)dυ, откуда f(υ)=
=f(υ)dυ, откуда f(υ)= 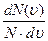 .
.
Применяя методы теории вероятностей, Максвелл нашел функцию f(υ):
f(υ)=4π 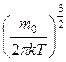 υ2
υ2 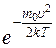 . (6.14)
. (6.14)
Из (6.14) видно, что конкретный вид функции зависит от рода газа (от массы m0 молекулы) и от параметра состояния (от температуры T). График функции (6.14) приведен на рис.6.6.
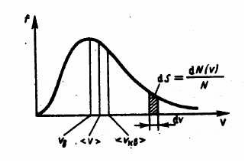
Рис.6.6
Относительное число молекул dΝ(υ)/Ν, скорости которых лежат в интервале от υ до υ+dυ, находится как площадь заштрихованной полоски. Площадь, ограниченная кривой распределения и осью абсцисс, равна 1. Это означает, что функция f(υ) удовлетворяет условию нормировки 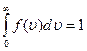 .
.
Скорость, при которой функция распределения молекул по скоростям максимальна, называется наиболее вероятной скоростью υв. Значение наиболее вероятной скорости можно найти, дифференцируя выражение (6.14) (постоянные множители опускаем) по аргументу υ, приравняв результат нулю и используя условие для максимума выражения f(υ):
υв = 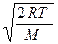 =
=  . (6.15)
. (6.15)
Средняя скорость молекулы <υ> (средняя арифметическая скорость) определяется по формуле
υc= 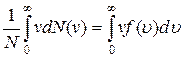 .
.
Подставляя сюда f(υ) и интегрируя, получаем:
υс= 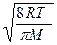 =
= 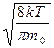 . (6.16)
. (6.16)
Исходя из распределения молекул по скоростям
dN(υ)= N f(υ)=N 4π 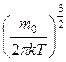 υ2
υ2 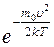 dV (6.17)
dV (6.17)
можно найти распределение молекул газа по кинетической энергии w.
Средняя кинетическая энергия молекулы идеального газа:
w = 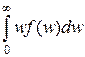 =
= 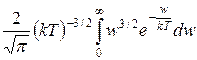 =
= 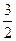 kT.
kT.
Дата добавления: 2015-06-17; просмотров: 1248;
